题目内容
18.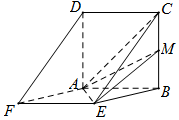 已知边长为2的正方形ABCD与菱形ABEF所在平面互相垂直,M为BC中点.
已知边长为2的正方形ABCD与菱形ABEF所在平面互相垂直,M为BC中点.(Ⅰ)求证:EM∥平面ADF.
(Ⅱ)若∠ABE=60°,求四面体M-ACE的体积.
分析 (Ⅰ)方法一:取AD中点N,连结MN.MN$\stackrel{∥}{=}$AB.证明EM∥NF.然后过证明EM∥平面ADF.
方法二:证明BC∥AD.说明BC∥平面ADF.通过证明平面BCE∥平面ADF.推出EM∥平面ADF.
(Ⅱ)方法一:取AB中点P,连结PE.证明EP⊥平面ABCD,然后利用等体积法求解即可.
方法二:取BE中点Q,连结AQ.说明AQ为四面体A-EMC的高.求出${S_{△EMC}}=\frac{1}{2}CM•BE=1$.利用等体积法求解体积即可.
解答 (本题满分9分)
(Ⅰ)方法一:
取AD中点N,连结MN.
∵四边形ABCD是正方形,M为BC中点,
∴MN$\stackrel{∥}{=}$AB.
∵四边形ABEF是菱形,∴AB$\stackrel{∥}{=}$EF.
∴MN$\stackrel{∥}{=}$EF.∴四边形MNFE是平行四边形.∴EM∥NF.
∵EM?平面ADF,NF?平面ADF,
∴EM∥平面ADF. …(5分)
方法二:
∵四边形ABCD是正方形,
∴BC∥AD.
∵BC?平面ADF,AD?平面ADF,
∴BC∥平面ADF.
∵四边形ABEF是菱形,
∴BE∥AF.
∵BE?平面ADF,AF?平面ADF,
∴BE∥平面ADF.
∵BC∥平面ADF,BE∥平面ADF,BC∩BE=B,
∴平面BCE∥平面ADF.
∵EM?平面BCE,
∴EM∥平面ADF.
(Ⅱ)方法一:
取AB中点P,连结PE.
∵在菱形ABEF中,∠ABE=60°,
∴△AEB为正三角形,
∴EP⊥AB.
∵AB=2,∴$EP=\sqrt{3}$.
∵平面ABCD⊥平面ABEF,
平面ABCD∩平面ABEF=AB,
∴EP⊥平面ABCD,
∴EP为四面体E-ACM的高.
∴${V_{M-ACE}}={V_{E-ACM}}=\frac{1}{3}{S_{△ACM}}•EP=\frac{1}{3}×\frac{1}{2}×1×2×\sqrt{3}=\frac{{\sqrt{3}}}{3}$. …(9分)
方法二:
取BE中点Q,连结AQ.
∵在菱形ABEF,∠ABE=60°,
∴△AEB为正三角形,
∴AQ⊥BE.
∵AB=2,∴$AQ=\sqrt{3}$.
∵四边形ABCD为正方形,
∴BC⊥AB.
∵平面ABCD⊥平面ABEF,∴BC⊥平面ABEF.
∵AQ?平面ABEF,BE?平面ABEF,
∴AQ⊥BC,BC⊥BE.
∴AQ⊥平面BEC.∴AQ为四面体A-EMC的高.
∵CB⊥EB,∴${S_{△EMC}}=\frac{1}{2}CM•BE=1$.
∴${V_{M-AEC}}={V_{A-EMC}}=\frac{1}{3}AQ•{S_{△EMC}}=\frac{1}{3}×\sqrt{3}×1=\frac{{\sqrt{3}}}{3}$. …(9分)
点评 本题考查几何体的体积的求法,直线与平面平行的判定定理以及性质定理的应用,等体积法的应用,考查空间想象能力以及计算能力.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案| A. | π | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{1}{2}$或$\frac{11}{32}$ | B. | $\frac{1}{2}$或$\frac{31}{32}$ | C. | $\frac{11}{32}$或$\frac{31}{32}$ | D. | $\frac{11}{32}$或$\frac{5}{2}$ |
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
| A. | (-∞,2) | B. | (2,+∞) | C. | (1,+∞) | D. | (4,+∞) |
