题目内容
若方程2|x|=9-x2 在区间(k,k+1)(k∈Z)上有解,则所有满足条件的实数k值的和为 .
考点:根的存在性及根的个数判断
专题:计算题,作图题,函数的性质及应用
分析:将方程的根化为f(x)=2|x|与g(x)=9-x2在区间(k,k+1)(k∈Z)上有交点,作出图象,由图可得k的值.
解答:
解:方程2|x|=9-x2 在区间(k,k+1)(k∈Z)上有解可化为:
f(x)=2|x|与g(x)=9-x2在区间(k,k+1)(k∈Z)上有交点,
作两个函数的简图如下:

则它们的交点在区间(-3,-2),(2,3)之间,
故k=-3,2;
故答案为:-1.
f(x)=2|x|与g(x)=9-x2在区间(k,k+1)(k∈Z)上有交点,
作两个函数的简图如下:

则它们的交点在区间(-3,-2),(2,3)之间,
故k=-3,2;
故答案为:-1.
点评:本题考查了方程的解与函数的零点之间的关系,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
抛物线将坐标平面分成两部分,我们将焦点所在的部分(不包括抛物线本身)称为抛物线的内部.若点N(a,b)在抛物线C:y2=2px(p>0)的内部,则直线l:by=p(x+a)与抛物线C的公共点的个数为( )
| A、0 | B、1 | C、2 | D、不能确定 |
某几何体的三视图如图所示,则该几何体的体积为( )
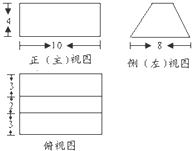

| A、240 | ||
| B、200 | ||
C、
| ||
D、
|