题目内容
如图，由曲线y=sinx，直线x=
π与x轴围成的阴影部分的面积是（ ）
| 3 |
| 2 |
| A、1 | ||
| B、2 | ||
C、2
| ||
| D、3 |
考点：定积分在求面积中的应用
专题：导数的综合应用
分析：利用定积分的几何意义以及正弦函数图象的特点，只要求定积分3
sinxdx即可．
| ∫ |
0 |
解答：
解：由已知由曲线y=sinx，直线x=
π与x轴围成的阴影部分的面积是3
sinxdx=3（-cosx）|
=3；
故选D
| 3 |
| 2 |
| ∫ |
0 |
0 |
故选D
点评：本题考查了定积分的几何意义，用来求曲边梯形的面积，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知AB为圆O的一条弦，且|AB|=2，则数量积
•
的值为（ ）
| AB |
| AO |
| A、2 | B、3 |
| C、4 | D、与圆的半径有关 |
已知函数f（x）=sin（2x+φ），其中φ为实数，且f（x）≤f（
）对x∈R恒成立．记P=f（
），Q=f（
），R=f（
），则P，Q，R的大小关系是（ ）
| 2π |
| 9 |
| 2π |
| 3 |
| 5π |
| 6 |
| 7π |
| 6 |
| A、R＜P＜Q |
| B、Q＜R＜P |
| C、P＜Q＜R |
| D、Q＜P＜R |
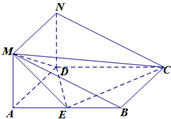如图所示的几何体中，四边形ABCD为菱形，AMND是矩形，平面AMND⊥平面ABCD，∠DAB=60°，AD=2，AM=1．下列结论成立的是（ ）
| A、若ac＞bc，则a＞b |
| B、若a＞b，则a2＞b2 |
| C、若a＞b，c＜d，则a+c＞b+d |
| D、若a＞b，c＞d，则a-d＞b-c |