题目内容
函数y=
的图象与函数y=2sinπx(-4≤x≤6)的图象所有交点的横坐标之和等于 .
| 1 |
| 1-x |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:先研究函数y=2sinπx与函数y=
的图象,画在同一坐标系中,再结合其对称性求出所有交点的横坐标之和.
| 1 |
| 1-x |
解答:
解:如图,做出函数y=2sin2πx,以及函数y=
的图象,并且它们的图象都关于点(1,0)对称,且当x=
时,y=sin2πx的图象在y=
的下方,
并且交点也关于(1,0)对称成对出现,每一对对称的点的横坐标的和为2,共6对,因此12个根的和为6×2=12.

| 1 |
| 1-x |
| 3 |
| 2 |
| 1 |
| 1-x |
并且交点也关于(1,0)对称成对出现,每一对对称的点的横坐标的和为2,共6对,因此12个根的和为6×2=12.

点评:本题有一定难度,一是图象的画法,涉及到了图象的平移变换,二是涉及到图象的对称,根(交点的横坐标)之间的关系.

练习册系列答案
相关题目
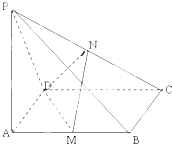 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD,M,N分别是AB,PC的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为1,M、N分别是对角线AD1、BD上的点,且AM=BN=x.
如图,已知正方体ABCD-A1B1C1D1的棱长为1,M、N分别是对角线AD1、BD上的点,且AM=BN=x.