题目内容
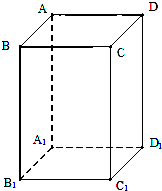 已知ABCD-A1B1C1D1是底面为正方形的直四棱柱,且A1B1=1,AA1=2,求:
已知ABCD-A1B1C1D1是底面为正方形的直四棱柱,且A1B1=1,AA1=2,求:(1)异面直线BD与AB1所成的角的余弦值;
(2)四面体AB1D1C1的体积.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:计算题,空间角
分析:(1)连接C1D、C1B,可得四边形AB1C1D是平行四边形,所以∠BDC1或其补角就是异面直线BD与AB1所成角.再利用余弦定理,即可求出异面直线BD与AB1所成的角的余弦值;
(2)根据题意,AA1⊥平面A1B1C1D1,即可求出四面体AB1D1C1的体积.
(2)根据题意,AA1⊥平面A1B1C1D1,即可求出四面体AB1D1C1的体积.
解答:
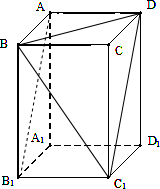 解:(1)连接C1D、C1B
解:(1)连接C1D、C1B
∵正四棱柱ABCD-A1B1C1D1中,AD∥B1C1且AD=B1C1,
∴四边形AB1C1D是平行四边形
因此AB1∥C1D,可得∠BDC1或其补角就是异面直线BD与AB1所成角
∵A1B1=1,AA1=2,∴BD=
,BC1=DC1=
,
∴cos∠BDC1=
=
,
即异面直线BD与AB1所成的角的余弦值为
;
(2)根据题意,AA1⊥平面A1B1C1D1,
∴四面体AB1D1C1的体积为
•
•1•1•2=
.
 解:(1)连接C1D、C1B
解:(1)连接C1D、C1B∵正四棱柱ABCD-A1B1C1D1中,AD∥B1C1且AD=B1C1,
∴四边形AB1C1D是平行四边形
因此AB1∥C1D,可得∠BDC1或其补角就是异面直线BD与AB1所成角
∵A1B1=1,AA1=2,∴BD=
| 2 |
| 5 |
∴cos∠BDC1=
| 2+5-5 | ||||
2•
|
| ||
| 10 |
即异面直线BD与AB1所成的角的余弦值为
| ||
| 10 |
(2)根据题意,AA1⊥平面A1B1C1D1,
∴四面体AB1D1C1的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题在正四棱柱中求异面直线所成角,并求四面体的体积,着重考查了正棱柱的性质、异面直线所成角和体积的求法等知识,属于基础题.

练习册系列答案
相关题目
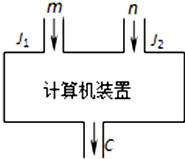 如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质:
如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质: