题目内容
解关于x的不等式:x2+ax+1<0.
考点:一元二次不等式的解法
专题:函数的性质及应用,不等式的解法及应用
分析:先计算出该不等式对应方程得判别式,然后通过讨论判别式的符号来判断该不等式对应函数与x轴的位置关系,然后根据图象写出不等式的解.
解答:
解:∵△=a2-4,
①当△>0,即a>2,或a<-2时,
由x2+ax+1=0得x=
,
此时原不等式的解为
<x<
,
②当△≤0,即-2≤a≤2时,原不等式无解.
综上所述,当a>2,或a<-2时,原不等式的解集为(
,
),
当-2≤a≤2时,原不等式的解集为∅.
①当△>0,即a>2,或a<-2时,
由x2+ax+1=0得x=
-a±
| ||
| 2 |
此时原不等式的解为
-a-
| ||
| 2 |
-a+
| ||
| 2 |
②当△≤0,即-2≤a≤2时,原不等式无解.
综上所述,当a>2,或a<-2时,原不等式的解集为(
-a-
| ||
| 2 |
-a+
| ||
| 2 |
当-2≤a≤2时,原不等式的解集为∅.
点评:解一元二次不等式的基本思想是函数思想、数形结合及分类讨论思想,讨论的依据一般是函数图象与x轴的位置关系,然后根据图象写出不等式的解.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
下列函数中,在区间(0,+∞)上是增函数的是( )
A、y=
| ||
B、y=
| ||
| C、y=-3x-2 | ||
D、y=(
|
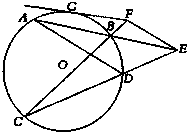 已知:如图,圆O两弦AB与CD交于E,EF∥AD,EF与CB延长线交于F,FG切圆O于G.
已知:如图,圆O两弦AB与CD交于E,EF∥AD,EF与CB延长线交于F,FG切圆O于G.