题目内容
若数列{2 an}是公比为q的等比数列，则（ ）
| A、{an}是公差为q的等差数列 |
| B、{an}是公差为2q的等差数列 |
| C、{an}是公差为log2q的等差数列 |
| D、{an}可能不是等差数列 |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：由题意，
=q，可得an+1-an=log2q，从而{an}是公差为log2q的等差数列
| 2an+1 |
| 2an |
解答：
解：由题意，
=q，
∴2an+1-an=q，
∴an+1-an=log2q，
∴{an}是公差为log2q的等差数列，
故选：C．
| 2an+1 |
| 2an |
∴2an+1-an=q，
∴an+1-an=log2q，
∴{an}是公差为log2q的等差数列，
故选：C．
点评：本题是一道考查数列概念方面较好的题目，既可以训练学生对通项公式的掌握，又可以训练学生判断数列属性的能力，属于概念考查类题目．
练习册系列答案
相关题目
设△ABC的内角A，B，C的对边分别为a，b，c，且a，b，c成等比数列，则角B的取值范围是（ ）
A、（0，
| ||
B、[
| ||
C、（0，
| ||
D、[
|
若f（x）与g（x）是定义在R上的可导函数，则“f′（x）=g′（x）”是“f（x）=g（x）”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
设双曲线
-
=1（a＞0，b＞0）的离心率为
，且它的一个焦点在抛物线y2=12x的准线上，则此双曲线的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
用数学归纳法证明“（n+1）（n+2）…（n+n）=2n•1•2…（2n-1）（n∈N+）时，从“n=k到n=k+1”时，左边应增添的式子是（ ）
| A、2k+1 |
| B、2k+3 |
| C、2（2k+1） |
| D、2（2k+3） |
i是虚数单位，若集合S={-2，0，1}，则（ ）
| A、i2015∈S | ||
| B、-2i2014∈S | ||
| C、i2013∈S | ||
D、i（i-
|
不等式|x-1|≥2的解集为（ ）
| A、{x|x≤-1或x≥3} |
| B、{x|x≥3} |
| C、{x|-1≤x≤3} |
| D、R |
如图，在半径为4，圆心角为变量2θ（0＜θ＜2π）的扇形OAB内作一内切圆P，再在扇形内作一个与扇形两半径相内切并与圆P外切的小圆Q，记圆Q的半径为y．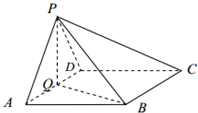
如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．