题目内容
4.在极坐标系中,△OAB的三边所在直线方程分别为$OA:θ=0,OB:θ=\frac{π}{2},AB:ρcos(θ-\frac{π}{3})=\sqrt{3}$,P为△OAB外接圆C上任一点,以极点O为原点,极轴为x轴的正半轴,取相同的单位长度建立直角坐标系.(1)在直角坐标系中,求点A、B的坐标和圆C的参数方程;
(2)求|PO|2+|PA|2+|PB|2的最大值和最小值.
分析 (1)直线OA:y=0.OB:x=0.直线AB:$ρ(\frac{1}{2}cosθ+\frac{\sqrt{3}}{2}sinθ)$=$\sqrt{3}$,利用互化公式可得直角坐标方程.可得A$(2\sqrt{3},0)$,B(0,2).利用中点坐标公式可得可得圆心M$(\sqrt{3},1)$.,利用两点之间的距离公式可得半径r=2.
可得外接圆的直角坐标方程,利用平方关系可得参数方程.
(2)设P$(\sqrt{3}+2cosθ,1+2sinθ)$.利用两点之间的距离公式可得:|PO|2+|PA|2+|PB|2=24+8$sin(θ+\frac{π}{3})$,即可得出.
解答 解:(1)直线OA:y=0.OB:x=0.直线AB:$ρ(\frac{1}{2}cosθ+\frac{\sqrt{3}}{2}sinθ)$=$\sqrt{3}$,化为:x+$\sqrt{3}y$-2$\sqrt{3}$=0.
∴A$(2\sqrt{3},0)$,B(0,2).
可得圆心M$(\sqrt{3},1)$.,半径r=$\frac{1}{2}\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=2.
∴外接圆的直角坐标方程为:$(x-\sqrt{3})^{2}$+(y-1)2=4,
可得参数方程为:$\left\{\begin{array}{l}{x=\sqrt{3}+2cosθ}\\{y=1+2sinθ}\end{array}\right.$(θ为参数).
(2)设P$(\sqrt{3}+2cosθ,1+2sinθ)$.
|PO|2+|PA|2+|PB|2=$(\sqrt{3}+2cosθ)^{2}$+(1+2sinθ)2+$(2cosθ-\sqrt{3})^{2}$+(1+2sinθ)2+$(\sqrt{3}+2cosθ)^{2}$+(2sinθ-1)2
=24+8$sin(θ+\frac{π}{3})$∈[16,32].
∴其最大值和最小值分别为32,16.
点评 本题考查了极坐标化为直角坐标、两点之间的距离公式、三角函数求值、和差公式、圆的标准方程与参数方程,考查了推理能力与计算能力,属于中档题.

| A. | {x|x<-1或x>1} | B. | {x|x<-2或x>2} | C. | {x|-1<x<1} | D. | {x|-2<x<2} |
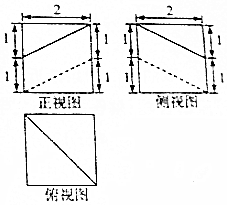 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{20}{3}$ | B. | $\frac{16}{3}$ | C. | 4 | D. | 7 |

| A. | 1.2 | B. | 0.6 | C. | 0.4 | D. | -0.4 |
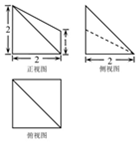
| A. | $\frac{10}{3}$ | B. | 4 | C. | $\frac{13}{3}$ | D. | 5 |
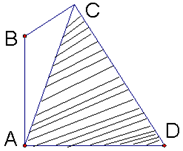 在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).
在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°). 如图所示函数图象,
如图所示函数图象,