题目内容
6.点P为直线y=$\frac{3}{4}$x上任一点,F1(-5,0),F2(5,0),则||PF1|-|PF2||的取值范围为[0,8.5].分析 由题意,P在原点时,||PF1|-|PF2||=0,求出F2(5,0)关于直线y=$\frac{3}{4}$x对称点的坐标,可得||PF1|-|PF2||的最大值,即可求出||PF1|-|PF2||的取值范围.
解答 解:由题意,P在原点时,||PF1|-|PF2||=0,
F2(5,0)关于直线y=$\frac{3}{4}$x对称点的坐标为F(a,b),则$\left\{\begin{array}{l}{\frac{b}{a-5}•\frac{3}{4}=-1}\\{\frac{b}{2}=\frac{3}{4}•\frac{a+5}{2}}\end{array}\right.$,∴a=$\frac{9}{5}$,b=$\frac{51}{10}$,
∴||PF1|-|PF2||的最大值为$\sqrt{(\frac{9}{5}+5)^{2}+(\frac{51}{10})^{2}}$=8.5,
∴||PF1|-|PF2||的取值范围为[0,8.5].
故答案为:[0,8.5].
点评 本题考查||PF1|-|PF2||的取值范围,考查对称性的运用,属于中档题.

练习册系列答案
相关题目
17.有一段“三段论”推理是这样的“对于可导函数f(x),如果f'(x0)=0,那么x=x0是函数f(x)的极值点;因为函数f(x)=x3在x=0处的导数值f'(x0)=0,所以x=0是函数f(x)=x3的极值点.”以上推理中:(1)大前提错误;(2)小前提错误;(3)推理形式正确;(4)结论正确.你认为正确的序号是( )
| A. | (1)(3) | B. | (2)(3) | C. | (1)(4) | D. | (2)(4) |
18.△ABC中,D为AB的中点,点F在线段CD(不含端点)上,且满足$\overrightarrow{AF}=x\overrightarrow{AB}+y\overrightarrow{AC}$(x,y∈R),则$\frac{1}{x}+\frac{2}{y}$的最小值为( )
| A. | $3+2\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | 6 | D. | 8 |
15.不等式x2-|x|-2<0(x∈R)的解集是( )
| A. | {x|x<-1或x>1} | B. | {x|x<-2或x>2} | C. | {x|-1<x<1} | D. | {x|-2<x<2} |
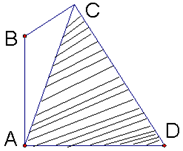 在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).
在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).