题目内容
3.△ABC中,$tanA=\frac{3}{4}$,则cos2A等于( )| A. | $\frac{18}{25}$ | B. | $-\frac{18}{25}$ | C. | $-\frac{7}{25}$ | D. | $\frac{7}{25}$ |
分析 利用同角三角函数的基本关系,二倍角公式,求得cos2A的值.
解答 解:△ABC中,∵$tanA=\frac{3}{4}$=$\frac{sinA}{cosA}$,sin2A+cos2A=1,∴sin2A=$\frac{9}{25}$,cos2A=$\frac{16}{25}$,
则cos2A=2cos2A-1=2•$\frac{16}{25}$-1=$\frac{7}{25}$,
故选:D.
点评 本题主要考查同角三角函数的基本关系,二倍角公式的应用,属于基础题.

练习册系列答案
相关题目
18.△ABC中,D为AB的中点,点F在线段CD(不含端点)上,且满足$\overrightarrow{AF}=x\overrightarrow{AB}+y\overrightarrow{AC}$(x,y∈R),则$\frac{1}{x}+\frac{2}{y}$的最小值为( )
| A. | $3+2\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | 6 | D. | 8 |
8.若当$\lim_{△x→0}\frac{{f({x_0})-f({x_0}+3△x)}}{2△x}$=1,则f′(x0)等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
15.不等式x2-|x|-2<0(x∈R)的解集是( )
| A. | {x|x<-1或x>1} | B. | {x|x<-2或x>2} | C. | {x|-1<x<1} | D. | {x|-2<x<2} |
12.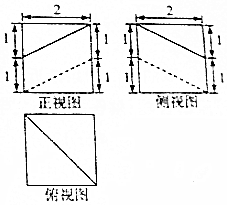 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{20}{3}$ | B. | $\frac{16}{3}$ | C. | 4 | D. | 7 |
13.已知一个几何体的三视图如图所示,则该几何体的体积为( )
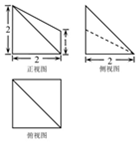

| A. | $\frac{10}{3}$ | B. | 4 | C. | $\frac{13}{3}$ | D. | 5 |
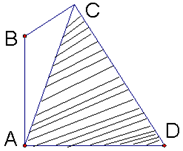 在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).
在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).