Question

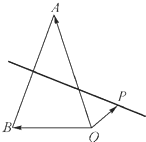如图，P为△AOB所在平面内一点，向量

OA

=

a

，

OB

=

b

，且点P在线段AB的垂直平分线上，向量

OP

=

c

．若|

a

|=3，|

b

|=2，则

.

c

•(

a

-

b

)的值为

 

．

Answer 1

考点：平面向量数量积的运算

专题：计算题,平面向量及应用

分析：设线段AB的垂直平分线为PH，H为垂足，求出向量OP，用向量a，b表示，再由向量的数量积的性质：向量的平方即为模的平方，和向量垂直的条件即为数量积为0，即可得到所求值．

解答： 解：设线段AB的垂直平分线为PH，H为垂足，
则

OP

=

OB

+

BH

+

HP

=

OB

+

1

2

BA

+

HP

=

OB

+

1

2

OA

-

1

2

OB

+

HP

=

1

2

OA

+

1

2

OB

+

HP

，
则

.

c

•(

a

-

b

)=（

1

2

OA

+

1

2

OB

+

HP

）•（

OA

-

OB

）
=

1

2

（

OA

2-

OB

2）+

HP

•

BA

=

1

2

×（3²-2²）+0=

5

2

．
故答案为：

5

2

．

点评：本题考查平面向量的数量积的性质：向量的平方即为模的平方，考查中点向量的表示，以及向量的加减运算，属于中档题．