题目内容
如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC.把△BAC沿AC折起到△PAC的位置,使得P点在平面ADC上的正投影O恰好落在线段AC上,如图2所示,点E、F分别为棱PC、CD的中点.
(1)求证:平面OEF∥平面APD;
(2)求证:CD⊥平面POF;
(3)若AD=3,CD=4,AB=5,求三棱锥E-CFO的体积.
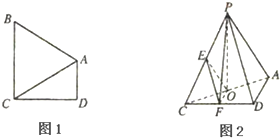
(1)求证:平面OEF∥平面APD;
(2)求证:CD⊥平面POF;
(3)若AD=3,CD=4,AB=5,求三棱锥E-CFO的体积.
考点:平面与平面平行的判定,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(1)证明平面OEF∥平面APD,只需证明OE∥平面PAD,OF∥平面PAD;
(2)证明CD⊥平面POF,只需证明OF⊥CD,PO⊥CD;
(3)求出以S△CFO=
S△ACD=
,E到平面CFO的距离为
,利用体积公式,即可求三棱锥E-CFO的体积.
(2)证明CD⊥平面POF,只需证明OF⊥CD,PO⊥CD;
(3)求出以S△CFO=
| 1 |
| 4 |
| 3 |
| 2 |
| 5 |
| 4 |
| 3 |
解答:
(1)证明:因为点P点在平面ADC上的正投影O恰好落在线段AC上,
所以PO⊥平面ABC,所以PO⊥AC …(1分)
因为AB=BC,
所以O是AC中点,…(2分)
所以OE∥PA,
因为PA?平面PAD
所以OE∥平面PAD…(3分)
同理OF∥平面PAD
又OE∩OF=O,OE、OF?平面OEF
所以平面OEF∥平面APD; …(5分)
(2)证明:因为OF∥AD,AD⊥CD
所以OF⊥CD
又PO⊥平面ADC,CD?平面ADC
所以PO⊥CD …(7分)
又OF∩PO=O
所以CD⊥平面POF; …(8分)
(3)解:因为∠ADC=90°,AD=3,CD=4,
所以S△ACD=
×3×4=6,
而点O,E分别是AC,CD的中点,
所以S△CFO=
S△ACD=
,…(10分)
由题意可知△ACP为边长为5的等边三角形,
所以高OP=
,…(11分)
即P点到平面ACD的距离为
,
又E为PC的中点,所以E到平面CFO的距离为
,
故VE-CFO=
×
×
=
.…(12分)
所以PO⊥平面ABC,所以PO⊥AC …(1分)
因为AB=BC,
所以O是AC中点,…(2分)
所以OE∥PA,
因为PA?平面PAD
所以OE∥平面PAD…(3分)
同理OF∥平面PAD
又OE∩OF=O,OE、OF?平面OEF
所以平面OEF∥平面APD; …(5分)
(2)证明:因为OF∥AD,AD⊥CD
所以OF⊥CD
又PO⊥平面ADC,CD?平面ADC
所以PO⊥CD …(7分)
又OF∩PO=O
所以CD⊥平面POF; …(8分)
(3)解:因为∠ADC=90°,AD=3,CD=4,
所以S△ACD=
| 1 |
| 2 |
而点O,E分别是AC,CD的中点,
所以S△CFO=
| 1 |
| 4 |
| 3 |
| 2 |
由题意可知△ACP为边长为5的等边三角形,
所以高OP=
| 5 |
| 2 |
| 3 |
即P点到平面ACD的距离为
| 5 |
| 2 |
| 3 |
又E为PC的中点,所以E到平面CFO的距离为
| 5 |
| 4 |
| 3 |
故VE-CFO=
| 1 |
| 3 |
| 3 |
| 2 |
| 5 |
| 4 |
| 3 |
| 5 |
| 8 |
| 3 |
点评:本题考查线面平行、面面平行,考查线面垂直,考查四棱锥E-CFO的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知实数x,y满足方程(x-2)2+y2=1,那么
的最大值为( )
| y |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.
如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C. 如图,AB是的⊙O直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE分别交⊙O于D、G两点,连接DG交CB于点F.
如图,AB是的⊙O直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE分别交⊙O于D、G两点,连接DG交CB于点F. 某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),
某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),