题目内容
已知函数y=sin2x+acosx-
a-
.
(1)当a=2时,求f(
);
(2)求函数的最大值为1时a的值.
| 1 |
| 2 |
| 3 |
| 2 |
(1)当a=2时,求f(
| π |
| 3 |
(2)求函数的最大值为1时a的值.
考点:三角函数中的恒等变换应用
专题:函数的性质及应用,三角函数的图像与性质
分析:(1)当a=2时,y=sin2x+2cosx-
.将x=
代入可得f(
);
(2)设cosx=t,函数解析式可化为y=-(t-
)2+
-
-
,-1≤t≤1.分当
<-1,即a<-2时,当-1≤
≤1时,即-2≤a≤2时,当
>1,即a>2时,三种情况讨论满足条件的a值,最后综合讨论结果,可得答案.
| 5 |
| 2 |
| π |
| 3 |
| π |
| 3 |
(2)设cosx=t,函数解析式可化为y=-(t-
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
解答:
解:(1)∵当a=2时,y=sin2x+2cosx-
.
∴f(
)=(
)2+2×
-
=-
,
(2)∵y=1-cos2x+acosx-
a-
=-cos2x+acosx-
-
=-(cosx-
)2+
-
-
.
设cosx=t,
∵-1≤cosx≤1,
∴-1≤t≤1.
∴y=-(t-
)2+
-
-
,-1≤t≤1.
1)当
<-1,即a<-2时,
此时当t=-1,y有最大值-
a-
.
由已知条件可得-
a-
=1,
∴a=-
>-2(舍去).
2)当-1≤
≤1时,即-2≤a≤2时,
此时当t=
,y有最大值
-
-
.
由已知条件可得
-
-
=1,
解得a=1-
或a=1+
(舍去).
3)当
>1,即a>2时,
此时当t=1,y有最大值
-
.
由已知条件可得
-
=1,
∴a=5.
综上可得a=1-
或a=5.
| 5 |
| 2 |
∴f(
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| 4 |
(2)∵y=1-cos2x+acosx-
| 1 |
| 2 |
| 3 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
| 1 |
| 2 |
设cosx=t,
∵-1≤cosx≤1,
∴-1≤t≤1.
∴y=-(t-
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
| 1 |
| 2 |
1)当
| a |
| 2 |
此时当t=-1,y有最大值-
| 3 |
| 2 |
| 3 |
| 2 |
由已知条件可得-
| 3 |
| 2 |
| 3 |
| 2 |
∴a=-
| 5 |
| 3 |
2)当-1≤
| a |
| 2 |
此时当t=
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
| 1 |
| 2 |
由已知条件可得
| a2 |
| 4 |
| a |
| 2 |
| 1 |
| 2 |
解得a=1-
| 7 |
| 7 |
3)当
| a |
| 2 |
此时当t=1,y有最大值
| a |
| 2 |
| 3 |
| 2 |
由已知条件可得
| a |
| 2 |
| 3 |
| 2 |
∴a=5.
综上可得a=1-
| 7 |
点评:本题考查的知识点是三角函数求值,二次函数在定区间上的最值问题,是三角函数与二次函数的综合应用,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)的图象向右平移1个单位长度后关于y轴对称,当x2>x1>-1时,
>0恒成立,设a=f(-2),b=f(-
),c=f(3),则a,b,c的大小关系为( )
| f(x2)-f(x1) |
| x2-x1 |
| 1 |
| 2 |
| A、c>a>b |
| B、c>b>a |
| C、a>c>b |
| D、b>a>c |
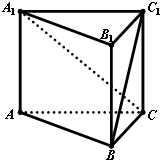 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<