题目内容
17.已知函数f(x)=2lnx-(x-1)2-2k(x-1).(Ⅰ)当k=1时,求f(x)的单调区间及极值;
(Ⅱ)确定实数k的取值范围,使得存在x0>1,当x∈(1,x0)时,恒有f(x)>0.
分析 (Ⅰ)首先求出函数的导数,利用函数单调性与导数的关系求单调区间以及极大值;
(Ⅱ)利用(Ⅰ)的结论,首先讨论k=1时是否满足题意;然后讨论k>1与k<1时函数的单调性与极值.
解答 解:(Ⅰ)当k=1时,f(x)=2lnx-(x-1)2-2(x-1)2lnx-x2+1,(x>0)
所以f'(x)=$\frac{2}{x}-2x$=$\frac{2(1+x)(1-x)}{x}$,
令f'(x)>0,得0<x<1,
令f'(x)=0得x=1,令f'(x)<0得x>1,
所以f(x)在(0,1)上的单调递增,在(1,+∞)单调递减;
当x=1时取极大值0;
(Ⅱ)由(Ⅰ)知,若k=1,当x>1时,f(x)<f(x)极大值=0,即不存在x0>1,当x∈(1,x0)时,恒有f(x)>0;
若k>1,当x>1时,f(x)=2lnx-(x-1)2-2k(x-1)<2lnx-(x-1)2-2(x-1)<0,即不存在x0>1,当x∈(1,x0)时,恒有f(x)>0;
若k<1,f(x)=2lnx-(x-1)2-2k(x-1).f'(x)=$\frac{2}{x}-2x+2-2k$=$\frac{2}{x}$[-x2+(1-k)x+1],
令f'(x)=0,即-x2+(1-k)x+1=0,解得x1=$\frac{k-1+\sqrt{(1-k)^{2}+4}}{-2}=\frac{1-k-\sqrt{(1-k)^{2}+4}}{2}$<0,
x2=$\frac{k-1-\sqrt{(1-k)^{2}+4}}{-2}$=$\frac{1-k+\sqrt{(1-k)^{2}+4}}{2}$>1,
所以当0<x<x2时,f'(x)>0,即f(x)在(0,x2)上是单调递增函数,所以在(1,x2)上是单调增函数,且f(1)=0,
所以存在x0>1,当x∈(1,x0)时,恒有f(x)>0.
综上k的取值范围是(-∞,1).
点评 本题考查了函数的大小与导数的关系;考查了讨论的数学思想;属于中档题.

| 年 份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 人口总数y | 8 | 8 | 8 | 9 | 9 | 10 | 11 |
| A. | (3,9) | B. | (9,3) | C. | (6,14) | D. | (4,11) |
 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )| A. | 24π | B. | $24π+8\sqrt{2}π$ | C. | $24π+4\sqrt{2}π$ | D. | 32π |
(Ⅰ)根据题目信息填写下表:
| 每吨产品 | 煤(吨) | 水(吨) | 电(千瓦) |
| A | |||
| B |
(Ⅲ)试问该企业利用现有资源,生产A、B两种产品各多少吨,才能获得最大利润?
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
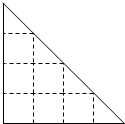 网上有一项虚似的游戏,在如图所示的等腰直角三角形上有15个格点(横、纵相邻格点间的距离为1个单位),三角形边界上的每个格点记1分,三角形内部的每个格点记2分,若点击鼠标左键,屏幕上会随机等可能地显示点中的某一格点,点中某格点后,将与其距离为1个单位的格点的分数和作为其得分.
网上有一项虚似的游戏,在如图所示的等腰直角三角形上有15个格点(横、纵相邻格点间的距离为1个单位),三角形边界上的每个格点记1分,三角形内部的每个格点记2分,若点击鼠标左键,屏幕上会随机等可能地显示点中的某一格点,点中某格点后,将与其距离为1个单位的格点的分数和作为其得分.