题目内容
一个中袋中装有大小相同,编号分别为1,2,3,4,5,6,7,8的八张卡片,现从中无放回地每次抽一张卡片,共抽2次,则取得两张卡片的编号和不小于14的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:基本事件总数n=
,取得两张卡片的编号和不小于14的基本事件个数m=2,由此能求出取得两张卡片的编号和不小于14的概率.
| C | 2 8 |
解答:
解:基本事件总数n=
=28,
取得两张卡片的编号和不小于14的基本事件个数m=2,
∴取得两张卡片的编号和不小于14的概率:
p=
=
.
故选:C.
| C | 2 8 |
取得两张卡片的编号和不小于14的基本事件个数m=2,
∴取得两张卡片的编号和不小于14的概率:
p=
| 2 |
| 28 |
| 1 |
| 14 |
故选:C.
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意古典概型概率计算公式的合理运用.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
已知条件p:x≠1或y≠2,条件q:xy≠2,那么¬p是¬q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知a,b为正实数,函数f(x)=ax3+bx+2在[0,1]上的最大值为4,则f(x)在[-1,0]上的最小值为( )
| A、0 | ||
B、
| ||
| C、-2 | ||
| D、2 |
学校为了了解高二年级教学情况,对全省班、实验班、普通班、中加班的学生做分层抽样调查.假设我校高二年级总人数为N,其中全省班有学生96人.若在全省班、实验班、普通班、中加班抽取的人数分别为12,21,25,43,则总人数N为( )
| A、801 | B、808 |
| C、853 | D、912 |
设x∈R,2 x2-1>4则不等式的解是( )
A、x≠±
| ||||
B、-
| ||||
| C、-2<x<2 | ||||
D、x>
|
已知函数f(x)=loga(2x+b-1)(a>0且a≠1)的图象如图所示,则a、b满足的关系式是( )
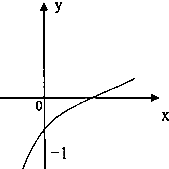

A、0<b<
| ||||
B、0<
| ||||
C、0<
| ||||
D、0<
|
直线l过点P(-2,0)且与圆x2+y2=1相切,则l的斜率是( )
| A、±1 | ||||
B、±
| ||||
C、±
| ||||
D、±
|
已知数列{an}通项公式为an=(-2)n,则在数列{an}的前10项中随机抽取一项,该项不小于8的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|