题目内容
已知数列{an}通项公式为an=（-2）n，则在数列{an}的前10项中随机抽取一项，该项不小于8的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型,等差数列的性质
专题：计算题,概率与统计
分析：由题意，数列{an}的前10项中，奇数项为负，偶数项为正，为4，16，64，256，1024，即可求出在数列{an}的前10项中随机抽取一项，该项不小于8的概率．
解答：
解：由题意，数列{an}的前10项中，奇数项为负，偶数项为正，为4，16，64，256，1024，
∴在数列{an}的前10项中随机抽取一项，该项不小于8的概率是
=
．
故答案为：
．
∴在数列{an}的前10项中随机抽取一项，该项不小于8的概率是
| 4 |
| 10 |
| 2 |
| 5 |
故答案为：
| 2 |
| 5 |
点评：本题考查概率的计算，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
一个中袋中装有大小相同，编号分别为1，2，3，4，5，6，7，8的八张卡片，现从中无放回地每次抽一张卡片，共抽2次，则取得两张卡片的编号和不小于14的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
三个数a=70.3，b=0.37，c=ln0.3的大小关系是（ ）
| A、a＞c＞b |
| B、a＞b＞c |
| C、b＞a＞c |
| D、c＞a＞b |
若α=kπ+
（k∈z），则α在（ ）
| π |
| 4 |
| A、第一、三象限 |
| B、第一、二象限 |
| C、第二、四象限 |
| D、第三、四象限 |
已知函数f（x）=
，则函数f（1）的值为（ ）
|
| A、-1 | B、0 | C、1 | D、4 |
i是虚数单位，
=（ ）
| 3-4i |
| 1+2i |
A、
| ||
B、
| ||
| C、-1+2i | ||
| D、-1-2i |
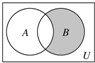已知全集U=N，A={0，1，2}，B={y|y=2x，x∈A}，则图中的阴影部分所表示的集合等于（ ）| A、{0} | B、{2} |
| C、{4} | D、{2，4} |
函数f（x）=x-4+log2x的零点所在的区间是（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |