题目内容
已知
=
,
=
,
=
且满足λ(
+
)•
=0(λ>0),则△ABC为( )
| BA |
| a |
| BC |
| b |
| AC |
| c |
| ||
|
|
| ||
|
|
| c |
| A、等腰三角形 | B、等边三角形 |
| C、直角三角形 | D、不确定 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用单位向量和向量的平行四边形法则可得:λ(
+
)表示与∠ABC的角平分线共线的向量,再利用λ(
+
)•
=0(λ>0),可知∠ABC的角平分线与边AC垂直.即可判断出.
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| c |
解答:
解:∵
,
分别表示与
,
共线的同向的单位向量,
∴λ(
+
)表示与∠ABC的角平分线共线的向量,
∵满足λ(
+
)•
=0(λ>0),
∴∠ABC的角平分线与边AC垂直.
因此△BAC是等腰三角形.
故选:A.
| ||
|
|
| ||
|
|
| BA |
| BC |
∴λ(
| ||
|
|
| ||
|
|
∵满足λ(
| ||
|
|
| ||
|
|
| c |
∴∠ABC的角平分线与边AC垂直.
因此△BAC是等腰三角形.
故选:A.
点评:本题考查了单位向量和向量的平行四边形法则、向量垂直与数量积的关系、等腰三角形的性质,属于难题.

练习册系列答案
相关题目
命题p:不等式
<0的解集为{x|0<x<1},命题q:“α=β”是“sinα=sinβ”成立的必要不充分条件,则( )
| x |
| x-1 |
| A、p真q假 |
| B、“p且q”为真 |
| C、“p或q”为假 |
| D、p假q真 |
若函数f(x+3)的定义域为[-5,-2],则F(x)=f(x+1)+f(x-1)的定义域为( )
| A、[-1,0] |
| B、[-1,1] |
| C、[0,1] |
| D、[-5,-2] |
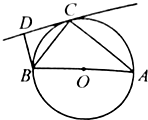 如图,⊙O的直径AB=4,C为圆周上一点,AC=3,CD是⊙O的切线,BD⊥CD于D,则CD=
如图,⊙O的直径AB=4,C为圆周上一点,AC=3,CD是⊙O的切线,BD⊥CD于D,则CD=