题目内容
10.设$\overrightarrow a=(\sqrt{3},1),\overrightarrow b=(x,-3)$,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则向量$\overrightarrow a-\overrightarrow b$的$\overrightarrow b$夹角为( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
分析 $\overrightarrow{a}$⊥$\overrightarrow{b}$,可得$\overrightarrow{a}•\overrightarrow{b}$=0,解得x.再利用向量夹角公式即可得出.
解答 解:∵$\overrightarrow{a}$⊥$\overrightarrow{b}$,∴$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{3}$x-3=0,解得x=$\sqrt{3}$.
∴$\overrightarrow a-\overrightarrow b$=(0,4),
∴($\overrightarrow a-\overrightarrow b$)•$\overrightarrow b$=-12,
|$\overrightarrow a-\overrightarrow b$|=4,$|\overrightarrow{b}|$=$\sqrt{(\sqrt{3})^{2}+(-3)^{2}}$=2$\sqrt{3}$,
设向量$\overrightarrow a-\overrightarrow b$的$\overrightarrow b$夹角为θ,
∴cosθ=$\frac{(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{a}-\overrightarrow{b}||\overrightarrow{b}|}$=$\frac{-12}{2\sqrt{3}×4}$=-$\frac{\sqrt{3}}{2}$,
∵$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ的取值范围是[0,π],
∴θ=150°.
故选:D.
点评 本题考查了向量垂直与数量积的关系、向量夹角公式,考查了推理能力与计算能力,属于中档题.

| 车流量(万辆) | 0~10 | 11~50 | 51~70 | 71~80 | 81~100 | >100 |
| 拥挤等级 | 优 | 良 | 轻度拥挤 | 中度拥挤 | 重度拥挤 | 严重拥挤 |
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 107日 |
| 车流量(万辆) | 120 | 110 | 85 | 75 | 60 | 105 | 110 |
(2)某人国庆节连续2天到该城市游玩,求这2天他遇到的车流量拥挤等级均为严重拥挤的概率.
| A. | 等差数列 | B. | 等比数列 | ||
| C. | 从第二项起为等差数列 | D. | 从第二项起为等比数列 |
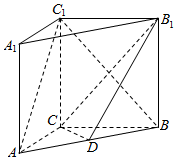 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.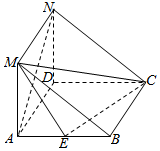 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点. 长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).