题目内容
1.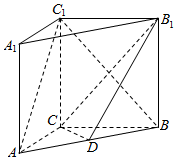 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求三棱锥D-AA1C1的体积.
分析 (1)由勾股定理的逆定理得AC⊥BC,由CC1⊥平面ABC得AC⊥CC1,故AC⊥平面BC1C,于是AC⊥BC1;
(2)设BC1与B1C的交点为E,连结DE,则由中位线定理得DE∥AC1,于是AC1∥平面CDB1;
(3)取AC中点M,连结DM,则DM⊥平面ACC1,故DM为棱锥D-AA1C1的高.
解答 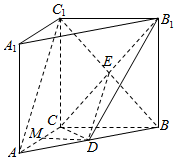 (1)证明:∵底面三边长AC=3,AB=5,BC=4,
(1)证明:∵底面三边长AC=3,AB=5,BC=4,
∴AC⊥BC,
∵AA1⊥底面ABC,AA1∥CC1,
∴CC1⊥平面ABC,∵AC?平面ABC,
∴AC⊥CC1,又BC∩CC1=C,BC?平面BCC1B1,CC1?平面BCC1B1,
∴AC⊥平面BCC1B1,∵BC1?平面BCC1B1,
∴AC⊥BC1.
(2)证明:设CB1与C1B的交点为E,连接DE,
∵D是AB的中点,E是BC1的中点,
∴DE∥AC1,
∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
(3)解:取AC的中点M,连接DM,
∵D是AB的中点,∴DM∥BC且$DM=\frac{1}{2}BC=2$.
又∵BC⊥AC,BC⊥AA1,∴BC⊥平面ACC1A1,
∴DM⊥平面ACC1A1.
∵${S_{△A{A_1}{C_1}}}=\frac{1}{2}A{A_1}•{A_1}{C_1}=\frac{1}{2}×4×3=6$,
∴${V_{D-A{A_1}{C_1}}}=\frac{1}{3}DM•{S_{△A{A_1}{C_1}}}=\frac{1}{3}×2×6=4$.
点评 本题考查了线面垂直的判定与性质,线面平行的判定,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
12.某校为调查2016届学业水平考试的数学成绩情况,随机抽取2个班各50名同学,得如下频率分布表:
(Ⅰ)估计甲,乙两班的数学平均分(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)数学成绩[60,70)为“C等”,[70,90)为“B等”和[90,100]为“A等”,从两个班成绩为“A等”的同学中用分层抽样的方法抽取5人,则甲乙两个班各抽取多少人?
(Ⅲ)从第(Ⅱ)问的5人中随机抽取2人,求这2人来自同一班级的概率.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 甲班频数 | 4 | 6 | 10 | 18 | 12 |
| 乙班频数 | 2 | 6 | 18 | 16 | 8 |
(Ⅱ)数学成绩[60,70)为“C等”,[70,90)为“B等”和[90,100]为“A等”,从两个班成绩为“A等”的同学中用分层抽样的方法抽取5人,则甲乙两个班各抽取多少人?
(Ⅲ)从第(Ⅱ)问的5人中随机抽取2人,求这2人来自同一班级的概率.
9.已知两条直线ax+y-2=0和3x+(a+2)y+1=0互相平行,则实数a等于( )
| A. | 1或-3 | B. | -1或3 | C. | 1或3 | D. | -1或-3 |
6.为了对某课题进行研究,用分层抽样的方法从三所高校A,B,C的相关人中抽取若干人组成研究小组,有关数据如下表(单位:人).
(1)求x,y;
(2)若从高校B,C抽取的人中选2人作专题发言,求这2人均来自高校C的概率.
| 高校 | 相关人数 | 抽取人数 |
| A | 54 | x |
| B | 36 | 2 |
| C | 72 | y |
(2)若从高校B,C抽取的人中选2人作专题发言,求这2人均来自高校C的概率.
10.设$\overrightarrow a=(\sqrt{3},1),\overrightarrow b=(x,-3)$,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则向量$\overrightarrow a-\overrightarrow b$的$\overrightarrow b$夹角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
11.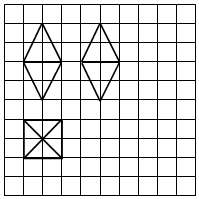 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )| A. | 16 | B. | 8$\sqrt{5}$ | C. | 32 | D. | 16$\sqrt{5}$ |
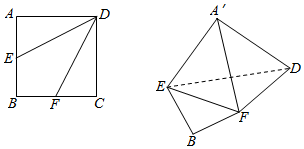 如图,边长为2的正方形ABCD中.
如图,边长为2的正方形ABCD中.