题目内容
19.数列{an}中,已知a1=1,S2=2,且Sn+1+2Sn-1=3Sn(n≥2,n∈N*),则数列{an}为( )| A. | 等差数列 | B. | 等比数列 | ||
| C. | 从第二项起为等差数列 | D. | 从第二项起为等比数列 |
分析 由已知求得a2=1,再由数列递推式变形得到an+1=2an(n≥2),即$\frac{{{a_{n+1}}}}{a_n}=2(n≥2)$,验证$\frac{a_2}{a_1}=1$不满足上式,可得数列{an}从第二项起为等比数列.
解答 解:由a1=1,S2=2,得a2=S2-a1=2-1=1,
由Sn+1+2Sn-1=3Sn,得Sn+1-Sn=2(Sn-Sn-1)(n≥2),
即an+1=2an(n≥2),
∴$\frac{{{a_{n+1}}}}{a_n}=2(n≥2)$,
又$\frac{a_2}{a_1}=1$不满足上式,
∴数列{an}从第二项起为等比数列.
故选:D.
点评 本题考查数列递推式,考查了等比关系的确定,是中档题.

练习册系列答案
相关题目
9.已知两条直线ax+y-2=0和3x+(a+2)y+1=0互相平行,则实数a等于( )
| A. | 1或-3 | B. | -1或3 | C. | 1或3 | D. | -1或-3 |
10.设$\overrightarrow a=(\sqrt{3},1),\overrightarrow b=(x,-3)$,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则向量$\overrightarrow a-\overrightarrow b$的$\overrightarrow b$夹角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
7.已知函数$f(x)=\left\{{\begin{array}{l}{3+{{log}_2}x,x>0}\\{2{x^2}-3x,x≤0}\end{array}}\right.$,则不等式f(x)≤5的解集为( )
| A. | [-1,1] | B. | (-∞,-1]∪(0,1) | C. | [-1,4] | D. | (-∞,-1]∪[0,4] |
4.f(x)=$\left\{\begin{array}{l}{\frac{\sqrt{x+1}-1}{x},x≠0}\\{0,x=0}\end{array}\right.$,则x=0是( )
| A. | 可去间断点 | B. | 无穷间断点 | C. | 连续点 | D. | 跳跃间断点 |
11.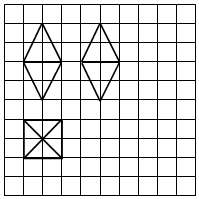 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )| A. | 16 | B. | 8$\sqrt{5}$ | C. | 32 | D. | 16$\sqrt{5}$ |
9.某公司为了增加其商品的销售利润,调查了该商品投入的广告费用x与销售利润y的统计数据如表:
由表中数据,得线性回归方程l:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$($\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$x),则下列结论错误的是( )
| 广告费用x(万元) | 2 | 3 | 5 | 6 |
| 销售利润y(万元) | 5 | 7 | 9 | 11 |
| A. | $\hat b>0$ | B. | $\hat a>0$ | C. | 直线l过点(4,8) | D. | 直线l过点(2,5) |
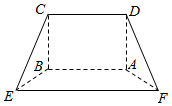 如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.
如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.