题目内容
20.某营养学家建议:高中生每天的蛋白质摄入量控制在[60,90](单位:克),脂肪的摄入量控制在[18,27](单位:克).某学校食堂提供的伙食以食物A和食物B为主,1千克食物A含蛋白质60克,含脂肪9克,售价20元;1千克食物B含蛋白质30克,含脂肪27克,售价15元.(Ⅰ)如果某学生只吃食物A,判断他的伙食是否符合营养学家的建议,并说明理由;
(Ⅱ)为了花费最低且符合营养学家的建议,学生需要每天同时食用食物A和食物B各多少千克?并求出最低需要花费的钱数.
分析 (Ⅰ)如果学生只吃食物Axkg,从而得不等式组$\left\{\begin{array}{l}{60≤60x≤90}\\{18≤9x≤27}\end{array}\right.$,是否有解即可;
(Ⅱ)由题意,设学生每天吃食物Axkg,食物Bykg;从而得到目标函数z=20x+15y;线性约束条件$\left\{\begin{array}{l}{60≤60x+30y≤90}\\{18≤9x+27y≤27}\\{x≥0}\\{y≥0}\end{array}\right.$,从而利用线性规划求解即可.
解答 解:(Ⅰ)如果学生只吃食物Axkg,
则$\left\{\begin{array}{l}{60≤60x≤90}\\{18≤9x≤27}\end{array}\right.$,
无解,
故不符合营养学家的建议;
(Ⅱ)由题意,设学生每天吃食物Axkg,食物Bykg;
则z=20x+15y;
$\left\{\begin{array}{l}{60≤60x+30y≤90}\\{18≤9x+27y≤27}\\{x≥0}\\{y≥0}\end{array}\right.$
作平面区域如下,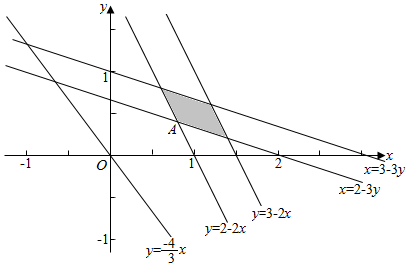 ,
,
由$\left\{\begin{array}{l}{x=2-3y}\\{y=2-2x}\end{array}\right.$解得,x=$\frac{4}{5}$,y=$\frac{2}{5}$;
故z=20×$\frac{4}{5}$+15×$\frac{2}{5}$=22;
答:学生每天吃0.8千克食物A,0.4千克食物B,既能符合营养学家的建议又花费最少.
最低需要花费22元.
点评 本题考查了线性规划在实际问题中的应用,属于中档题.

练习册系列答案
相关题目
10.设$\overrightarrow a=(\sqrt{3},1),\overrightarrow b=(x,-3)$,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则向量$\overrightarrow a-\overrightarrow b$的$\overrightarrow b$夹角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
11.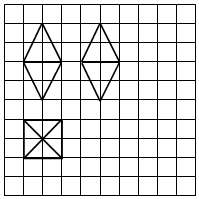 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )| A. | 16 | B. | 8$\sqrt{5}$ | C. | 32 | D. | 16$\sqrt{5}$ |
12.曲线y=e${\;}^{\frac{1}{3}x}$在点(6,e2)处的切线与坐标轴所围成的三角形的面积为( )
| A. | $\frac{3}{2}{e}^{2}$ | B. | 3e2 | C. | 6e2 | D. | 9e2 |
9.某公司为了增加其商品的销售利润,调查了该商品投入的广告费用x与销售利润y的统计数据如表:
由表中数据,得线性回归方程l:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$($\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$x),则下列结论错误的是( )
| 广告费用x(万元) | 2 | 3 | 5 | 6 |
| 销售利润y(万元) | 5 | 7 | 9 | 11 |
| A. | $\hat b>0$ | B. | $\hat a>0$ | C. | 直线l过点(4,8) | D. | 直线l过点(2,5) |
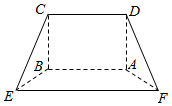 如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.
如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.