题目内容
已知函数f(x)=x2-1,g(x)=a|x-1|
(Ⅰ)若函数φ(x)=|f(x)|-g(x)只有一个零点,求实数a的取值范围;
(Ⅱ)当a≥-3时,求函数h(x)=|f(x)|+g(x)在区间[-2,1]上的最大值.
(Ⅰ)若函数φ(x)=|f(x)|-g(x)只有一个零点,求实数a的取值范围;
(Ⅱ)当a≥-3时,求函数h(x)=|f(x)|+g(x)在区间[-2,1]上的最大值.
考点:函数最值的应用,函数的零点
专题:综合题,导数的综合应用
分析:(1)方程|f(x)|=g(x)可化为|x-1|(|x+1|-a)=0,易知x=1已是该方程的根,从而要使原方程只有一解,即要求方程|x+1|=a有且仅有一个等于1的解或无解,结合图象可得a的范围;
(2)当a≥-3时,求出函数h(x)=|f(x)|+g(x)的解析式,根据分段函数最值的求法,分别求出各断上函数的最值,然后求出它们的最大值即可.
(2)当a≥-3时,求出函数h(x)=|f(x)|+g(x)的解析式,根据分段函数最值的求法,分别求出各断上函数的最值,然后求出它们的最大值即可.
解答:
解:(1)函数φ(x)=|f(x)|-g(x)只有一个零点,即|x2-1|=a|x-1|,变形得|x-1|(|x+1|-a)=0,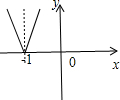
显然,x=1已是该方程的根,从而要使原方程只有一解,即要求方程|x+1|=a有且仅有一个等于1的解或无解,
作出函数y=|x+1|的图象如图所示:
结合图形得a<0.
(2)h(x)=|f(x)|+g(x)=)=|x2-1|+a|x-1|
=
,
当-2≤x<-1时,
≥-
,当x=-2时,h(x)的最大值为h(-2)=3a+3;
当-1≤x≤1时,h(x)的最大值为max{h(-1),h(1),h(-
)}=max{0,
a2+a+1,2a}=
a2+a+1.

显然,x=1已是该方程的根,从而要使原方程只有一解,即要求方程|x+1|=a有且仅有一个等于1的解或无解,
作出函数y=|x+1|的图象如图所示:
结合图形得a<0.
(2)h(x)=|f(x)|+g(x)=)=|x2-1|+a|x-1|
=
|
当-2≤x<-1时,
| a |
| 2 |
| 3 |
| 2 |
当-1≤x≤1时,h(x)的最大值为max{h(-1),h(1),h(-
| a |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题考查函数的零点和二次函数在定区间上的最值问题,其中求出函数的解析式是关键,求出分段函数在各断上的最值,再比较大小是难点,考查运算能力和分类讨论的数学思想.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目