题目内容
已知圆C过点P(
,
),且与圆M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.
(Ⅰ)求圆C的方程;
(Ⅱ)设Q为圆C上的一个动点,求
•
的最小值;
(Ⅲ)过点P作两条相异直线分别与圆C相交于A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
| ||
| 2 |
| ||
| 2 |
(Ⅰ)求圆C的方程;
(Ⅱ)设Q为圆C上的一个动点,求
| PQ |
| MQ |
(Ⅲ)过点P作两条相异直线分别与圆C相交于A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
考点:直线与圆的位置关系,平面向量数量积的运算,圆的标准方程
专题:直线与圆
分析:(Ⅰ)设圆心C(a,b),由已知得
,由此得圆C的方程为x2+y2=r2,将点P的坐标代入,能示出圆C的方程.
(2)设Q(x,y),则x2+y2=1,且
•
=(x-1,y-1)•(x+2,y+2)=x2+y2+x+y-4=x+y-3,由此利用圆的参数方程能求出
•
的最小值.
(3)由题意知直线PA与直线PB的斜率存在,且互为相反数,由已知条件求出xA=
•
,xB=
•
,从而推导出kAB=kOP,进而得到直线OP和直线AB一定平行.
|
(2)设Q(x,y),则x2+y2=1,且
| PQ |
| MQ |
| PQ |
| MQ |
(3)由题意知直线PA与直线PB的斜率存在,且互为相反数,由已知条件求出xA=
| ||
| 2 |
| k2-2k-1 |
| 1+k2 |
| ||
| 2 |
| k2+2k-1 |
| 1+k2 |
解答:
解:(Ⅰ)设圆心C(a,b),
则
,解得a=0,b=0,
∴圆C的方程为x2+y2=r2,
将点P的坐标代入,得r2=1,
故圆C的方程为x2+y2=1.
(2)设Q(x,y),则x2+y2=1,
且
•
=(x-1,y-1)•(x+2,y+2)=x2+y2+x+y-4=x+y-3,
∵
,
∴
•
=cosθ+sinθ-3=
sin(θ+
)-3,
∴
•
的最小值为-3-
;
(3)由题意知直线PA与直线PB的斜率存在,且互为相反数,
故设PA:y-
=k(x-
),PB:y-
=-k(x-
),
由
,得(1+k2)x2+
k(1-k)x+
(1-k)2-1=0,
∵点P的横坐标为x=
一定是该方程的解,故得xA=
•
,
同理xB=
•
,
∴kAB=
=
=
=1=kOP,
∴直线OP和直线AB一定平行.
则
|
∴圆C的方程为x2+y2=r2,
将点P的坐标代入,得r2=1,
故圆C的方程为x2+y2=1.
(2)设Q(x,y),则x2+y2=1,
且
| PQ |
| MQ |
∵
|
∴
| PQ |
| MQ |
| 2 |
| π |
| 4 |
∴
| PQ |
| MQ |
| 2 |
(3)由题意知直线PA与直线PB的斜率存在,且互为相反数,
故设PA:y-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
由
|
| 2 |
| 1 |
| 2 |
∵点P的横坐标为x=
| ||
| 2 |
一定是该方程的解,故得xA=
| ||
| 2 |
| k2-2k-1 |
| 1+k2 |
同理xB=
| ||
| 2 |
| k2+2k-1 |
| 1+k2 |
∴kAB=
| yB-yA |
| xB-xA |
-k(xB-
| ||||||||
| xB-xA |
=
| ||
| xB-xA |
∴直线OP和直线AB一定平行.
点评:本题考查圆的方程的求法,考查向量的数量积的最小值的求法,考查直线OP和AB是否平行的判断,解题时要认真审题,注意圆的参数方程的合理运用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
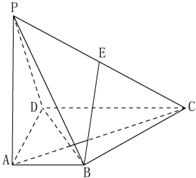 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.