题目内容
已知函数f(x)=1-2sin2
.
(Ⅰ)在区间[
,
]上任取x0,求满足f(x0)≥
的概率;
(Ⅱ)若f(α)=
,α为第四象限角,求
的值.
| x |
| 2 |
(Ⅰ)在区间[
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
(Ⅱ)若f(α)=
2
| ||
| 3 |
| sin(π-2α)+cos(π+α) |
| tanα |
考点:二倍角的余弦,几何概型,运用诱导公式化简求值
专题:三角函数的图像与性质
分析:(Ⅰ)利用二倍角公式求出f(x0)≥
的x的范围,利用几何概型求解概率即可;
(Ⅱ)通过f(α)=
,α为第四象限角,利用同角三角函数的基本关系式求解sinα,利用诱导公式直接化简求解
的值.
| 1 |
| 2 |
(Ⅱ)通过f(α)=
2
| ||
| 3 |
| sin(π-2α)+cos(π+α) |
| tanα |
解答:
解:(Ⅰ)f(x)=1-2sin2
=cosx…(1分)
当x0∈[-
,
],满足f(x0)≥
的范围是[-
,
]…(3分)
由几何概型可知满足f(x0)≥
的概率是P=
=
…(5分)
(Ⅱ)由题意可得cosα=
,α为第四象限角,所以sinα=-
,tanα=-
,…(7分)
所以
=
=
…(9分)
=
…(10分)
| x |
| 2 |
当x0∈[-
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
由几何概型可知满足f(x0)≥
| 1 |
| 2 |
| ||||
|
| 2 |
| 3 |
(Ⅱ)由题意可得cosα=
2
| ||
| 3 |
| 1 |
| 3 |
| 1 | ||
2
|
所以
| sin(π-2α)+cos(π+α) |
| tanα |
| sin2α-cosα |
| tanα |
| 2sinαcosα-cosα |
| tanα |
| sin(π-2α)+cos(π+α) |
| tanα |
| 40 |
| 9 |
点评:本题考查二倍角公式的应用,诱导公式的应用,几何概型,考查计算能力.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
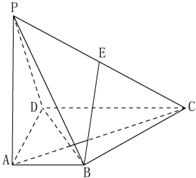 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.