题目内容
现有含三个元素的集合，既可以表示为{a，
，1}，也可表示为{a2，a+b，0}，则a2013+b2013=（ ）
| b |
| a |
| A、-1 | B、0 | C、1 | D、2 |
考点：集合的相等
专题：集合
分析：由题意得：{a，
，1}={a2，a+b，0}，由a为分母可得：a≠0，进而
=0，即b=0，a2=1≠a，解得a，b值后，代入可得答案．
| b |
| a |
| b |
| a |
解答：
解：由题意得：{a，
，1}={a2，a+b，0}，
∵a≠0，
∴
=0，故b=0，
∴a2=1≠a，
解得：a=-1，
故a2013+b2013=-1，
故选：A
| b |
| a |
∵a≠0，
∴
| b |
| a |
∴a2=1≠a，
解得：a=-1，
故a2013+b2013=-1，
故选：A
点评：本题考查的知识点是集合相等，从特殊元素入手分析，是解答此类问题的关键．
练习册系列答案
相关题目
已知函数f（x）=2sin（
x+
），则f（1）+f（2）+…+f（2012）+f（2013）的值是（ ）
| π |
| 3 |
| 2π |
| 3 |
A、-2
| ||
B、-
| ||
C、
| ||
| D、0 |
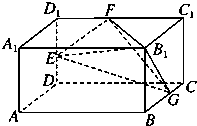如图，长方体AC1中，AB=2，BC=AA1=1．E、F、G分别为棱DD1、D1C1、BC的中点．