题目内容
在“天宫一号”发射成功后,我国将发射神州八号,并且我国已和欧洲签署合作协议,将在神州八号上为欧洲空间局搭载生物实验样品,假设他们计划搭载的样品为A,B,根据该样品的研制成本,样品重量、搭载实验费用和预计生产的收益来决定具体安排,通过调查,有关数据如表:
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
| 产品A(件) | 产品B(件) | ||
| 研制成本与搭载费用之和(万元/件) | 20 | 30 | 计划最大资金额300万元 |
| 样品重量(千克/件) | 10 | 5 | 最大搭载重量110千克 |
| 预计收益(万元/件) | 80 | 60 |
考点:简单线性规划的应用
专题:计算题,数形结合,不等式的解法及应用
分析:设安排产品A为x件,产品B为y件,总预计收益为z万元,由题意列出满足条件的不等式组,然后利用线性规划求解总预计收益的最大值.
解答:
解:设安排产品A为x件,产品B为y件,总预计收益为z万元,
则
,
z=80x+60y.
由约束条件作出可行域如图,

化目标函数z=80x+60y为y=-
x+
,
由图可知,当直线y=-
x+
过点B(9,4)时,
目标函数z=80x+60y取得最大值为z=80×9+60×4=960万元.
故最大收益为960万元.
则
|
z=80x+60y.
由约束条件作出可行域如图,

化目标函数z=80x+60y为y=-
| 4 |
| 3 |
| z |
| 60 |
由图可知,当直线y=-
| 4 |
| 3 |
| z |
| 60 |
目标函数z=80x+60y取得最大值为z=80×9+60×4=960万元.
故最大收益为960万元.
点评:本题考查了简单的线性规划问题,考查了数学建模思想方法,训练了利用线性规划求函数的最值,是中档题.

练习册系列答案
相关题目
已知AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR等于( )
| A、30° |
| B、300或1500 |
| C、1500 |
| D、以上都不对 |
如果圆柱的体积是16π,底面直径与母线长相等,则底面圆的半径为( )
| A、2 | B、4 | C、6 | D、8 |
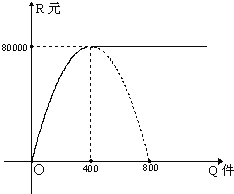 某工厂生产某种产品,固定成本为20000元,每生产一件产品,成本增加100元.已知总收益R是年产量Q(件)的函数,其图象(图中实线部分)如下:当年产量Q在[0,400]内时,为抛物线的一段;当年产量Q>400件时,为一条射线.
某工厂生产某种产品,固定成本为20000元,每生产一件产品,成本增加100元.已知总收益R是年产量Q(件)的函数,其图象(图中实线部分)如下:当年产量Q在[0,400]内时,为抛物线的一段;当年产量Q>400件时,为一条射线.