题目内容
已知数列{an}的前n项和Sn满足:Sn=a(Sn-an+1)(正常数a≠1),cn=
-
.
(1)求{an}的通项公式;
(2)设bn=an2+Sn•an,若数列{bn}为等比数列,求a的值;
(3)在满足条件(2)的情形下,cn=
-
,数列{cn}的前n项和为Tn,求证:Tn>2n-
.
| 1 |
| an+1 |
| 1 |
| an+1-1 |
(1)求{an}的通项公式;
(2)设bn=an2+Sn•an,若数列{bn}为等比数列,求a的值;
(3)在满足条件(2)的情形下,cn=
| 1 |
| an+1 |
| 1 |
| an+1-1 |
| 1 |
| 2 |
考点:数列的求和,数列递推式
专题:
分析:(Ⅰ)利用数列{an}的通项an与前n项和Sn之间的关系:n=1时,a1=s1;n≥2时,an=sn-sn-1,即可求出数列{an}的通项an.
(Ⅱ)将通项an代入已知条件Sn=a(Sn-an+1)即可求出Sn的表达式,将an与Sn代入bn的表达式,据已知条件数列{bn}为等比数列,利用b22=b1b3即可求出a的值.
(Ⅲ)由已知得cn=
-
=2-
+
,从而得到cn>2-
+
,由此能证明Tn>2n-
.
(Ⅱ)将通项an代入已知条件Sn=a(Sn-an+1)即可求出Sn的表达式,将an与Sn代入bn的表达式,据已知条件数列{bn}为等比数列,利用b22=b1b3即可求出a的值.
(Ⅲ)由已知得cn=
| 1 | ||
(
|
| 1 | ||
(
|
| 1 |
| 2n+1 |
| 1 |
| 2n+1-1 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2 |
解答:
(Ⅰ)解:当n=1时,S1=a(S1-a1+1),∴a1=a,
当n≥2时,Sn=a(Sn-an+1),Sn-1=a(Sn-1-an-1+1)
两式相减得:an=a•an-1,
=a(a≠0,n≥2),
即{an}是等比数列,
∴
=a•an-1=an.
(Ⅱ)解:由a≠1得bn=an2+Sn•an
=(an)2+
•an=
,
若{bn}为等比数列,则有b22=b1b3,
而b1=2a2,b2=a3(2a+1),b3=a4(2a2+a+1),
故[a3(2a+1)]2=2a2•a4(2a2+a+1),
解得a=
,
再将a=
代入bn得bn=(
)n,即数列{bn}是等比数列,
∴a=
.
(Ⅲ)证明:由(Ⅱ)知an=(
)n,又cn=
-
,
∴cn=
-
=2-
+
,
∴cn>2-
+
,
Tn=c1+c2+…+cn
>(2-
+
)+(2-
+
)+…+(2-
+
)
=2n-
+
>2n-
.
∴Tn>2n-
.
当n≥2时,Sn=a(Sn-an+1),Sn-1=a(Sn-1-an-1+1)
两式相减得:an=a•an-1,
| an |
| an-1 |
即{an}是等比数列,
∴
| a | n |
(Ⅱ)解:由a≠1得bn=an2+Sn•an
=(an)2+
| a(an-1) |
| a-1 |
| (2a-1)a2n-a•an |
| a-1 |
若{bn}为等比数列,则有b22=b1b3,
而b1=2a2,b2=a3(2a+1),b3=a4(2a2+a+1),
故[a3(2a+1)]2=2a2•a4(2a2+a+1),
解得a=
| 1 |
| 2 |
再将a=
| 1 |
| 2 |
| 1 |
| 2 |
∴a=
| 1 |
| 2 |
(Ⅲ)证明:由(Ⅱ)知an=(
| 1 |
| 2 |
| 1 |
| an+1 |
| 1 |
| an+1-1 |
∴cn=
| 1 | ||
(
|
| 1 | ||
(
|
=2-
| 1 |
| 2n+1 |
| 1 |
| 2n+1-1 |
∴cn>2-
| 1 |
| 2n |
| 1 |
| 2n+1 |
Tn=c1+c2+…+cn
>(2-
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
=2n-
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
∴Tn>2n-
| 1 |
| 2 |
点评:本题考查了数列{an}的通项公式an与前n项和Sn之间的关系,及等比数列的通项公式.较好地检验了学生应用基础知识解决问题的能力.

练习册系列答案
相关题目
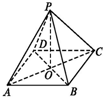 如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,运用三段论证明BD⊥平面PAC.
如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,运用三段论证明BD⊥平面PAC.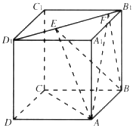 如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=