题目内容
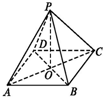 如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,运用三段论证明BD⊥平面PAC.
如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,运用三段论证明BD⊥平面PAC.考点:进行简单的演绎推理
专题:推理和证明
分析:运用三段论先证明PO⊥BD,AC⊥BD;再证明BD⊥平面PAC.
解答:
证明:大前提:如果一条直线与一个平面垂直,那么这条直线垂直于平面内的任意一条直线,
小前提:PO⊥平面ABCD,BD?平面ABCD,
结论:PO⊥BD;
大前提:正方形的对角线互相垂直,
小前提:AC、BD是正方形ABCD的对角线,
结论:AC⊥BD;
大前提:如果一条直线垂直于平面内的两条相交直线,那么这条直线与该平面垂直,
小前提:PO⊥BD,AC⊥BD,PO∩AC=O,且PO?平面PAC,AC?平面PAC,
结论:BD⊥平面PAC.
小前提:PO⊥平面ABCD,BD?平面ABCD,
结论:PO⊥BD;
大前提:正方形的对角线互相垂直,
小前提:AC、BD是正方形ABCD的对角线,
结论:AC⊥BD;
大前提:如果一条直线垂直于平面内的两条相交直线,那么这条直线与该平面垂直,
小前提:PO⊥BD,AC⊥BD,PO∩AC=O,且PO?平面PAC,AC?平面PAC,
结论:BD⊥平面PAC.
点评:本题通过空间中的线面垂直的证明,考查了演绎推理的三段论的应用问题,也考查了逻辑思维能力,是一道比较好的考查基础知识的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
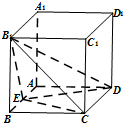 如图,正方体ABCD-A1B1C1D1中,E是AB的中点
如图,正方体ABCD-A1B1C1D1中,E是AB的中点(Ⅰ)求二面角D-B1E-C的平面角的余弦值.
(Ⅱ)在B1C上是否存在点P,使PB∥平面B1ED,若存在,求出点P的位置,若不存在,请说明理由.
 根据如图所示算法语句,将输出的A值依次分别记为a1,a2,…,an,…,a2014
根据如图所示算法语句,将输出的A值依次分别记为a1,a2,…,an,…,a2014 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90,点D是棱B1C1的中点.