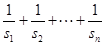题目内容
已知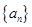 是递增的等差数列,
是递增的等差数列, ,
,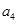 是方程
是方程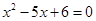 的根。
的根。
(I)求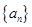 的通项公式;
的通项公式;
(II)求数列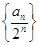 的前
的前 项和.
项和.
(1) ;(2)
;(2)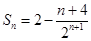 .
.
解析试题分析:(1)根据题中所给一元二次方程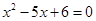 ,可运用因式分解的方法求出它的两根为2,3,即可得出等差数列中的
,可运用因式分解的方法求出它的两根为2,3,即可得出等差数列中的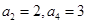 ,运用等差数列的定义求出公差为d,则
,运用等差数列的定义求出公差为d,则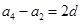 ,故
,故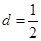 ,从而
,从而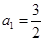 .即可求出通项公式;(2)由第(1)小题中已求出通项,易求出:
.即可求出通项公式;(2)由第(1)小题中已求出通项,易求出: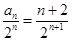 ,写出它的前n项的形式:
,写出它的前n项的形式: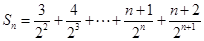 ,观察此式特征,发现它是一个差比数列,故可采用错位相减的方法进行数列求和,即两边同乘
,观察此式特征,发现它是一个差比数列,故可采用错位相减的方法进行数列求和,即两边同乘 ,即:
,即: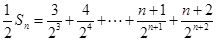 ,将两式相减可得:
,将两式相减可得: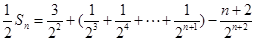
 ,所以
,所以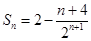 .
.
试题解析:(1)方程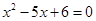 的两根为2,3,由题意得
的两根为2,3,由题意得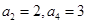 .
.
设数列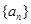 的公差为d,则
的公差为d,则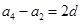 ,故
,故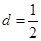 ,从而
,从而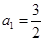 .
.
所以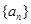 的通项公式为
的通项公式为 .
.
(2)设 的前n项和为
的前n项和为 ,由(1)知
,由(1)知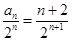 ,则
,则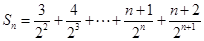 ,
,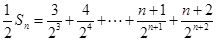 .
.
两式相减得

所以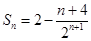 .
.
考点:1.一元二次方程的解法;2.等差数列的基本量计算;3.数列的求和

练习册系列答案
相关题目
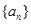 满足:
满足: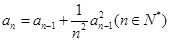
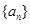 是以常数
是以常数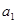 为首项,公差也为
为首项,公差也为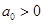 ,求证:
,求证: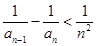 对任意
对任意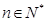 都成立;
都成立;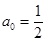 ,求证:
,求证: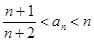 对任意
对任意 为等差数列,且
为等差数列,且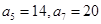 ,数列
,数列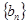 的前
的前 项和为
项和为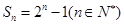 ,
,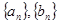 的通项公式;
的通项公式;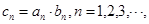 ,求数列
,求数列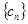 的前
的前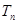 .
. 的前
的前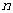 项和为
项和为 ,且
,且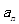 是
是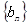 满足
满足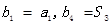 .
.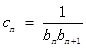 ,数列
,数列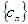 的前n项和为
的前n项和为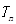 ,若
,若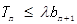 对一切
对一切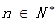 恒成立,求实数
恒成立,求实数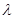 的最小值.
的最小值.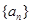 的公差为
的公差为 ,点
,点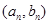 在函数
在函数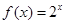 的图象上(
的图象上( ).
).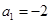 ,点
,点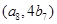 在函数
在函数 的图象上,求数列
的图象上,求数列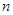 项和
项和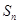 ;
;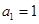 ,学科网函数
,学科网函数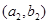 处的切线在
处的切线在 轴上的截距为
轴上的截距为 ,求数列
,求数列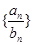 的前
的前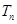 .
.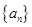 满足
满足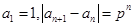 ,
,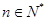 .
.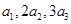 成等差数列,求
成等差数列,求 的值;
的值;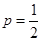 ,且
,且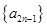 是递增数列,
是递增数列,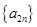 是递减数列,求数列
是递减数列,求数列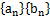 (
(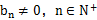 ),满足
),满足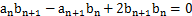 .
.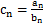 ,求数列
,求数列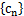 的通项公式;
的通项公式;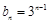 ,求数列
,求数列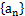 的前n项和
的前n项和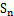
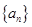 满足
满足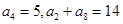 ,数列
,数列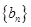 满足
满足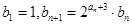 。
。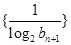 的前
的前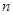 项和;
项和;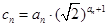 ,求数列
,求数列 的前
的前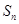
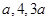 ,前
,前 项的和为
项的和为 .
.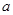 ;
;