题目内容
已知数列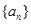 满足:
满足: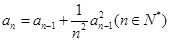
(1)若数列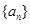 是以常数
是以常数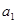 为首项,公差也为
为首项,公差也为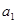 的等差数列,求
的等差数列,求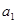 的值;
的值;
(2)若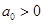 ,求证:
,求证: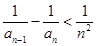 对任意
对任意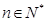 都成立;
都成立;
(3)若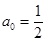 ,求证:
,求证: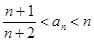 对任意
对任意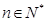 都成立;
都成立;
(1)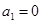 ;(2)(3)证明如下.
;(2)(3)证明如下.
解析试题分析:(1)由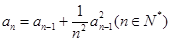 得:
得: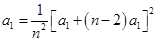 ,从而可求出
,从而可求出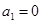 ;
;
(2)由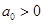 得
得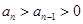 ,则
,则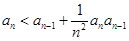 ,两边同除以
,两边同除以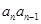 即可证明;(3)由(2)可知
即可证明;(3)由(2)可知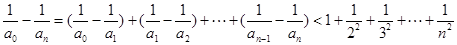 ,再进行放缩可证得结论.
,再进行放缩可证得结论.
试题解析:(1)由题意,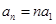 ,又由
,又由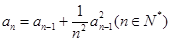 得
得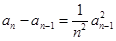 ,
,
即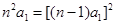 ,
,
∴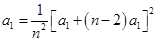 ,即
,即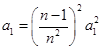 对一切
对一切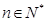 成立,所以
成立,所以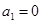 ;
;
(2)由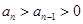 得
得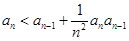 ,
,
两边同除以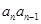 得
得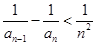 ;
;
(3)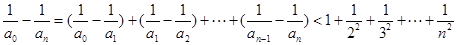
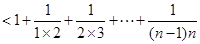
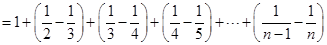
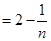 ,
,
将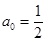 代入,得
代入,得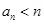 ,①
,①
由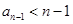 得
得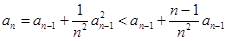 ,
,
所以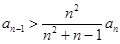 ,
,
所以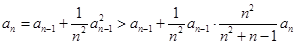 ,
,
所以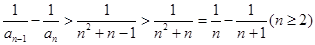
从而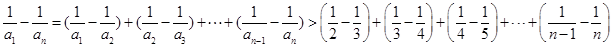
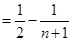 ,
,
又由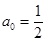 得
得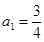 ,
,
所以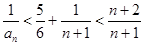 ,
,
从而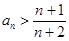 ,②
,②
由①②可得,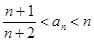 .
.
考点:1、数列及其性质;2、放缩法.

练习册系列答案
相关题目
 中,
中,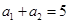 ,
,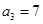 ,记数列
,记数列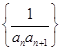 的前
的前 项和为
项和为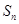 .
. 、
、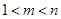 ,使得
,使得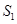 、
、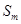 、
、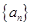 是等差数列,
是等差数列,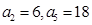 ,数列
,数列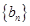 的前
的前 项和为
项和为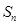 ,且
,且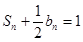 .
.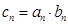 ,若
,若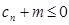 对任意的
对任意的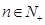 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.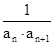 ,数列{bn}的前n项和为Tn,求Tn的最小值.
,数列{bn}的前n项和为Tn,求Tn的最小值.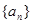 ,满足
,满足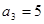 且
且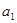 ,
,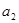 ,
,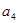 成等比数列.
成等比数列.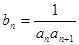 ,求数列
,求数列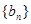 前
前 项的和为
项的和为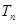 .
. 的前
的前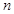 项和记为
项和记为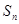 .已知
.已知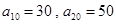 ,
,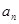 ;(2)若
;(2)若 ,求
,求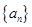 是递增的等差数列,
是递增的等差数列, ,
,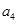 是方程
是方程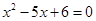 的根。
的根。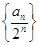 的前
的前 项和.
项和. 的前
的前 项和为
项和为 ,则
,则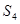 ,
,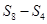 ,
,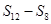 ,
,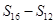 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列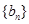 的前
的前 ,则
,则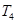 , ,______,
, ,______,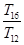 成等比数列.
成等比数列.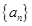 为等差数列,
为等差数列,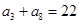 ,
,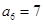 ,则
,则 ____________
____________