题目内容
已知数列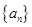 满足
满足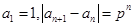 ,
,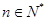 .
.
(1)若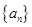 为递增数列,且
为递增数列,且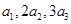 成等差数列,求
成等差数列,求 的值;
的值;
(2)若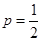 ,且
,且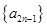 是递增数列,
是递增数列,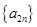 是递减数列,求数列
是递减数列,求数列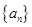 的通项公式.
的通项公式.
(1)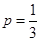 (2)
(2) 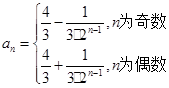 或
或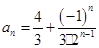
解析试题分析:(1)利用数列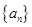 的单调性,得到
的单调性,得到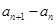 的符号去掉
的符号去掉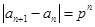 的绝对值,再分布令
的绝对值,再分布令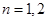 得到
得到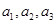 之间的关系,再利用题目已知等差中项的性质列出关于
之间的关系,再利用题目已知等差中项的性质列出关于 的等式,即可求出
的等式,即可求出 的值.
的值.
(2)根据数列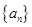 在
在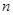 为奇数和偶数的单调性可得到
为奇数和偶数的单调性可得到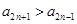 且
且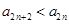 ,两不等式变为同号相加即可得到
,两不等式变为同号相加即可得到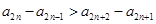 ,根据题意可得
,根据题意可得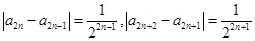 结合
结合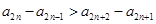 与
与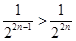 可去掉
可去掉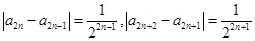 的绝对值,分
的绝对值,分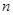 为奇或偶数,利用叠加法即可求出数列
为奇或偶数,利用叠加法即可求出数列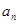 的通项公式.
的通项公式.
(1)因为数列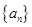 为递增数列,所以
为递增数列,所以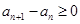 ,则
,则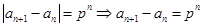 ,分别令
,分别令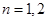 可得
可得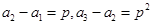
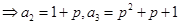 ,因为
,因为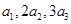 成等差数列,所以
成等差数列,所以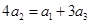
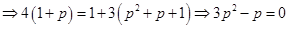
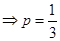 或
或 ,
,
当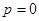 时,数列
时,数列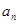 为常数数列不符合数列
为常数数列不符合数列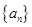 是递增数列,所以
是递增数列,所以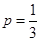 .
.
(2)由题可得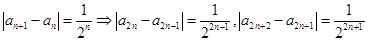 ,因为
,因为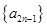 是递增数列且
是递增数列且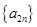 是递减数列,所以
是递减数列,所以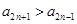 且
且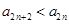 ,则有
,则有 ,因为
,因为
(2)由题可得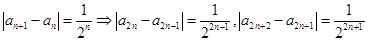 ,因为
,因为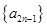 是递增数列且
是递增数列且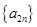 是递减数列,所以
是递减数列,所以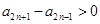 且
且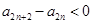
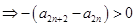 ,两不等式相加可得
,两不等式相加可得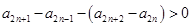
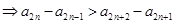 ,
,
又因为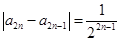
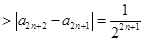 ,所以
,所以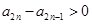 ,即
,即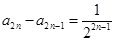 ,
,
同理可得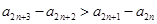 且
且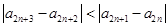 ,所以
,所以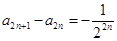 ,
,
则当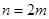
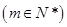 时,
时,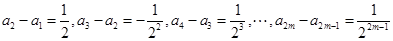 ,这
,这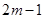 个等式相加可得
个等式相加可得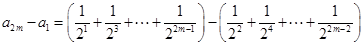
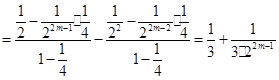
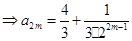 .
.
当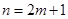 时,
时, 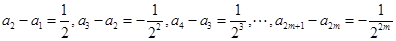 ,这
,这 个等式相加可得
个等式相加可得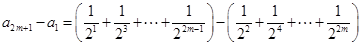
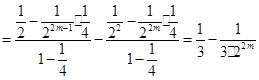
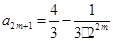 ,当
,当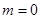 时,
时,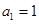 符合,故
符合,故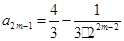
综上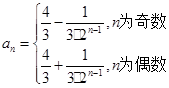

练习册系列答案
相关题目
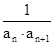 ,数列{bn}的前n项和为Tn,求Tn的最小值.
,数列{bn}的前n项和为Tn,求Tn的最小值. 是首项
是首项 的递增等差数列,
的递增等差数列,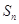 为其前
为其前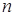 项和,且
项和,且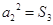 .
.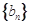 满足
满足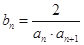 ,
,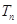 为数列
为数列 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.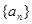 的前
的前 项和为
项和为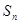 ,
,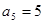 ,
,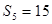 ,
,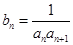 ,求数列
,求数列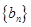 的前100项和.
的前100项和.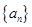 是递增的等差数列,
是递增的等差数列, ,
,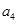 是方程
是方程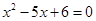 的根。
的根。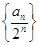 的前
的前 项和.
项和.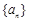 的公差
的公差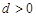 ,设
,设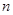 项和为
项和为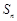 ,
,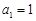 ,
,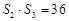
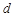 及
及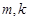 (
(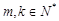 )的值,使得
)的值,使得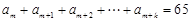 .
.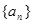 满足
满足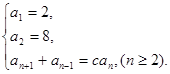 (
( 为常数,
为常数,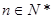 )
)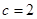 时,求
时,求 ;
;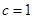 时,求
时,求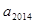 的值;
的值; 恒成立的常数
恒成立的常数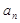 }中,
}中, ,前
,前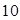 项和
项和 .
.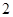 项、第
项、第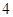 项、第
项、第 项…第
项…第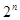 项……按原来的顺序组成一个新的数列{
项……按原来的顺序组成一个新的数列{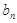 },求数列{
},求数列{ 项和
项和 .
. 的前n项和.
的前n项和.  , 且对所有正整数n, 有
, 且对所有正整数n, 有 . 判断
. 判断