题目内容
数列 的前
的前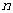 项和为
项和为 ,且
,且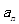 是
是 和1的等差中项,等差数列
和1的等差中项,等差数列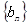 满足
满足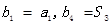 .
.
(1)求数列 ,
,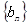 的通项公式;
的通项公式;
(2)设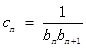 ,数列
,数列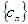 的前n项和为
的前n项和为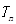 ,若
,若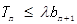 对一切
对一切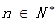 恒成立,求实数
恒成立,求实数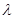 的最小值.
的最小值.
(1) 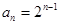 ,
,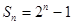 (2)
(2) 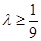
解析试题分析:本类问题属于已知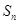 求
求 问题,解决此类问题的方法是
问题,解决此类问题的方法是 ,但是所求的通项公式是从第二项开始,要注意验证
,但是所求的通项公式是从第二项开始,要注意验证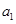 是否等于
是否等于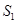 .(2) 等差数列型是数列求和中常见的类型,它的特点是
.(2) 等差数列型是数列求和中常见的类型,它的特点是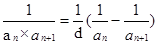 ,解决的方法是先进行裂项
,解决的方法是先进行裂项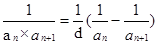 ,然后在求和,求和时应该注意余下的项前后位置是对称的,符号是相反的.对于恒成立问题,分离变量是一种常用的方法,因此本题可以采用此方法将
,然后在求和,求和时应该注意余下的项前后位置是对称的,符号是相反的.对于恒成立问题,分离变量是一种常用的方法,因此本题可以采用此方法将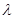 和n进行分离,然后利用函数的思想进行求解.
和n进行分离,然后利用函数的思想进行求解.
(1)∵ 是
是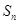 和1的等差中项,∴
和1的等差中项,∴
当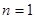 时,
时, ,∴
,∴
当 时,
时, ,
,
∴ ,即
,即 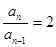
∴数列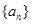 是以
是以 为首项,2为公比的等比数列, ∴
为首项,2为公比的等比数列, ∴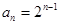 ,
,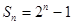
设 的公差为d,
的公差为d,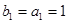 ,
, ,∴
,∴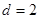
∴
(2)
∴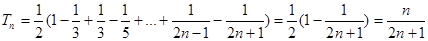
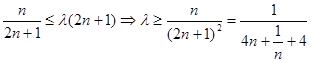
由 得:
得:
令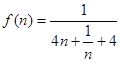 ,可知f(n)单调递减,即
,可知f(n)单调递减,即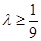 .
.
考点:1.等差等比数列2.数列求和3.函数的单调性.

练习册系列答案
相关题目
 中,
中,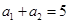 ,
,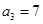 ,记数列
,记数列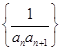 的前
的前 项和为
项和为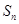 .
. 、
、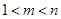 ,使得
,使得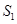 、
、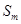 、
、 的前
的前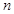 项和记为
项和记为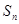 .已知
.已知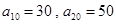 ,
,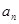 ;(2)若
;(2)若 ,求
,求 是首项
是首项 的递增等差数列,
的递增等差数列,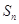 为其前
为其前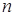 项和,且
项和,且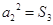 .
.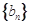 满足
满足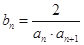 ,
,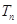 为数列
为数列 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.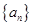 的前n项和为
的前n项和为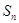 ,且满足条件
,且满足条件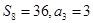
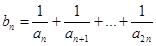 ,若对任意正整数
,若对任意正整数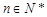 ,
, 恒成立,求
恒成立,求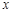 的取值范围.
的取值范围.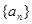 的前
的前 项和为
项和为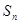 ,
,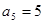 ,
,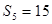 ,
,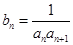 ,求数列
,求数列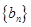 的前100项和.
的前100项和.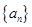 是递增的等差数列,
是递增的等差数列, ,
,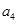 是方程
是方程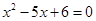 的根。
的根。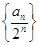 的前
的前 项和.
项和.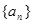 满足
满足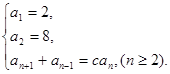 (
( 为常数,
为常数,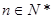 )
)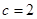 时,求
时,求 ;
;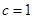 时,求
时,求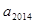 的值;
的值; 恒成立的常数
恒成立的常数