题目内容
已知等差数列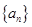 满足
满足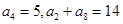 ,数列
,数列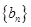 满足
满足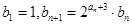 。
。
(1)求数列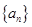 和
和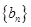 的通项公式;
的通项公式;
(2)求数列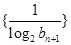 的前
的前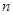 项和;
项和;
(3)若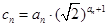 ,求数列
,求数列 的前
的前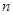 项和
项和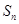
(1) ;
; (2)
(2) ;(3)
;(3)
解析试题分析:(1)设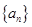 的首项为
的首项为 ,公差为
,公差为 ,由
,由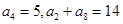 ,解出
,解出 ,
, 即可,数列
即可,数列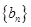 满足
满足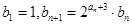 ,由
,由 ,
, ,
, ,以上各式相乘,
,以上各式相乘, ,
, ,可得
,可得
(2)设数列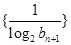 的前
的前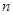 项和为
项和为 ,裂项可得
,裂项可得 ,易得
,易得 .
.
(3)由 ,显然利用错位相减法可得数列
,显然利用错位相减法可得数列 的前
的前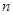 项和
项和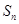
(1)设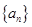 的首项为
的首项为 ,公差为
,公差为 ,由
,由 ,
, ;数列
;数列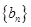 满足
满足 ,
, ,
, ,以上各式相乘,得
,以上各式相乘,得 ,
, ,
,
故 ;
;
(2) ,
,
由裂项求和法
(3) ,利用错位相减法可得
,利用错位相减法可得



考点:等差、等比数列的通项,裂项求和法,错位相减法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前
的前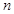 项和记为
项和记为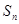 .已知
.已知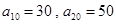 ,
,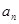 ;(2)若
;(2)若 ,求
,求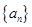 是递增的等差数列,
是递增的等差数列, ,
,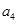 是方程
是方程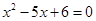 的根。
的根。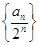 的前
的前 项和.
项和.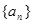 满足
满足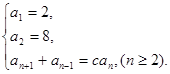 (
( 为常数,
为常数,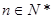 )
)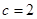 时,求
时,求 ;
;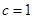 时,求
时,求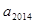 的值;
的值; 恒成立的常数
恒成立的常数 满足:
满足: ,且
,且 、
、 、
、 成等比数列.
成等比数列. 为数列
为数列 项和,是否存在正整数
项和,是否存在正整数 若存在,求
若存在,求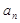 }中,
}中, ,前
,前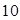 项和
项和 .
.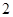 项、第
项、第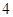 项、第
项、第 项…第
项…第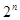 项……按原来的顺序组成一个新的数列{
项……按原来的顺序组成一个新的数列{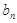 },求数列{
},求数列{ 项和
项和 .
.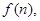 试写出
试写出 的表达式;
的表达式;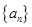 为正项等比数列,
为正项等比数列,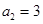 ,
,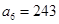 ,
,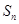 为等差数列
为等差数列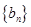 的前
的前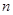
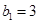 ,
,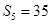 .
.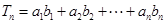 ,求
,求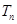 .
.