题目内容
7.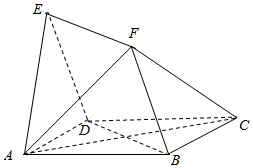 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.(1)求证:AC⊥平面BDEF;
(2)求三棱锥E-ABD的体积.
分析 (1)设AB,CD交于点O,根据菱形的性质可得AC⊥BD,由FA=FC可得AC⊥FO,故而AC⊥平面BDEF;
(2)根据菱形的性质计算OA,BD,DE,∠BDE,得出S△BDE,则VE-ABD=VA-BDE=$\frac{1}{3}{S}_{△BDE}$•OA.
解答  (1)证明:设AB∩CD=O,连接DF,OF
(1)证明:设AB∩CD=O,连接DF,OF
∵四边形ABCD为菱形,
∴AC⊥BD,
∵AF=CF,O为AC的中点,
∴AC⊥OF,
又∵BD?平面BDEF,OF?平面BDEF,BD∩OF=O,
∴AC⊥平面BDEF.
(2)解:四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,
∴DE=BD=2,∠BDE=120°,OA=$\sqrt{3}$.
∴S△BDE=$\frac{1}{2}BD×DE×sin120°$=$\sqrt{3}$,
由(1)得AC⊥平面BDEF,
所以AO⊥平面BDEF,
∴VE-ABD=VA-BDE=$\frac{1}{3}{S}_{△BDE}$•OA=$\frac{1}{3}×\sqrt{3}×\sqrt{3}$=1.
点评 本题考查了线面垂直的判定,菱形的性质,棱锥的体积计算,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
1.掷两颗匀称骰子,得到2点的概率是( )
| A. | $\frac{1}{36}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
18.等差数列{an}中,已知a3=10,a8=-20,则公差d等于( )
| A. | 3 | B. | -6 | C. | 4 | D. | -3 |
12.以坐标原点为对称中心,两坐标轴为对称轴的双曲线C的一条渐近线的斜率为$\sqrt{3}$,则双曲线C的离心率为( )
| A. | 2或$\sqrt{3}$ | B. | 2或$\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | 2 |