题目内容
1.掷两颗匀称骰子,得到2点的概率是( )| A. | $\frac{1}{36}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 试验发生包含的事件是掷两颗骰子有6×6=36个结果,满足条件的事件是向上点数2的只有1种结果,得到概率.
解答 解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件是掷两颗骰子有6×6=36个结果,2点的只有1种结果,
故要求的概率是P=$\frac{1}{36}$,
故选:A.
点评 本题考查等可能事件的概率,本题解题的关键是列举出满足条件的事件数,列举时要做到不重不漏,本题是一个基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
8.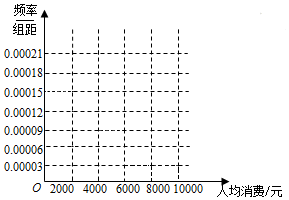 某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:
某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:
(1)做出这些数据的频率分布直方图并估计次境外旅游线路游客的人均购物的消费平均值;
(2)在调查问卷中有一项是“您会资助失学儿童的金额?”,调查情况如表,请补全如表,并说明是否有95%以上的把握认为资助数额多于或少于500元和自身购物是否到4000元有关?
附:临界值表参考公式:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
 某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:
某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:| 人均购物消费情况 | [0,2000] | (2000,4000] | (4000,6000] | (6000,8000] | (8000,10000] |
| 额数 | 15 | 20 | 9 | 3 | 3 |
(2)在调查问卷中有一项是“您会资助失学儿童的金额?”,调查情况如表,请补全如表,并说明是否有95%以上的把握认为资助数额多于或少于500元和自身购物是否到4000元有关?
| 人均购物消费不超过4000元 | 人均购物消费超过4000元 | 合计 | |
| 资助超过500元 | 30 | ||
| 资助不超过500元 | 6 | ||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
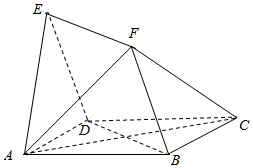 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.