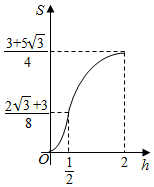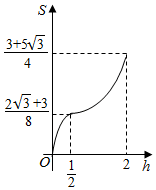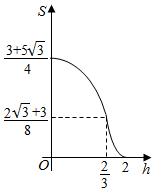题目内容
18.等差数列{an}中,已知a3=10,a8=-20,则公差d等于( )| A. | 3 | B. | -6 | C. | 4 | D. | -3 |
分析 设该等差数列的公差为d,首项为a1,根据题意可得a3=a1+2d=10①以及a8=a1+7d=-20②;联立①、②可得d的值,即可得答案.
解答 解:根据题意,设该等差数列的公差为d,首项为a1,
则有a3=a1+2d=10,①
a8=a1+7d=-20,②
②-①可得:5d=-30,
即d=-6;
故选:B.
点评 本题考查等差数列的通项公式,关键是依据等差数列的通项公式,构造关于公差d的方程组.

练习册系列答案
相关题目
4.设函数f(x)=$\left\{\begin{array}{l}cosπx,x>0\\ f(x+1)-1,x≤0\end{array}$,则f(-$\frac{4}{3}$)的值为( )
| A. | $-\frac{3}{2}$ | B. | $\frac{{\sqrt{3}}}{2}-2$ | C. | $-\frac{{\sqrt{3}}}{2}-2$ | D. | $-\frac{5}{2}$ |
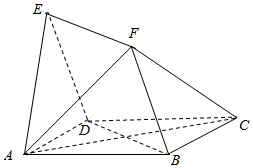 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.
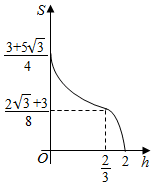
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.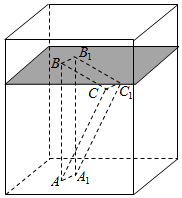 已知三棱柱ABC-A1B1C1,侧棱BB1⊥平面ABC,AB=2,AC=$\sqrt{3}$,AA1=$\frac{1}{4}$,AC⊥BC,将其放入一个水平放置的水槽中,使AA1在水槽底面内,平面ABB1A1与水槽底面垂直,且水面恰好经过棱BB1,现水槽底面出现一个洞,水位下降,则在水位下降过程中,几何体露出水面部分的面积S关于水位下降的高度h的图象大致为( )
已知三棱柱ABC-A1B1C1,侧棱BB1⊥平面ABC,AB=2,AC=$\sqrt{3}$,AA1=$\frac{1}{4}$,AC⊥BC,将其放入一个水平放置的水槽中,使AA1在水槽底面内,平面ABB1A1与水槽底面垂直,且水面恰好经过棱BB1,现水槽底面出现一个洞,水位下降,则在水位下降过程中,几何体露出水面部分的面积S关于水位下降的高度h的图象大致为( )