题目内容
已知奇函数f(x)是R上的减函数,且f(3)=-2,设P={x||f(x+t)-1|<1},Q={x|f(x)<-2},若“x∈Q”是“x∈P”的必要不充分条件,则实数t的取值范围是 .
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数的单调性求出P,Q的等价条件,利用充分条件和必要条件的定义即可得到结论.
解答:
解:∵奇函数f(x)是R上的减函数,且f(3)=-2,
∴不等式f(x)<-2等价为f(x)<f(3),解得x<3,即Q={x|x<3},
由|f(x+t)-1|<1得-1<f(x+t)-1<1,
解得0<f(x+t)<2,
则不等式等价为f(0)<f(x+t)<-f(3)=f(-3),
解得-3<x+t<0,
即-t-3<x<-t,
即P={x|-t-3<x<-t},
若“x∈Q”是“x∈P”的必要不充分条件,
则P?Q,
即-t≤3,
解得t≥-3.
故答案为:[-3,+∞)
∴不等式f(x)<-2等价为f(x)<f(3),解得x<3,即Q={x|x<3},
由|f(x+t)-1|<1得-1<f(x+t)-1<1,
解得0<f(x+t)<2,
则不等式等价为f(0)<f(x+t)<-f(3)=f(-3),
解得-3<x+t<0,
即-t-3<x<-t,
即P={x|-t-3<x<-t},
若“x∈Q”是“x∈P”的必要不充分条件,
则P?Q,
即-t≤3,
解得t≥-3.
故答案为:[-3,+∞)
点评:本题主要考查充分条件和必要条件的应用,根据函数的单调性和奇偶性的关系进行转化是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知a,b,a+b成等差数列,a,b,ab成等比数列,且logc(ab)>1,则c的取值范围是( )
| A、0<c<1 |
| B、1<c<8 |
| C、c>8 |
| D、0<c<1或c>8 |
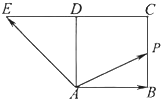 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中