题目内容
8．
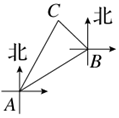如图，某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发，沿北偏东60°方向进行海面巡逻，当航行半小时到达B处时，发现北偏西45°方向有一艘船C，若船C位于A的北偏东30°方向上，则缉私艇所在的B处与船C的距离是（ ）km．| A． | 5（$\sqrt{6}$+$\sqrt{2}$） | B． | 5（$\sqrt{6}$-$\sqrt{2}$） | C． | 10（$\sqrt{6}$+$\sqrt{2}$） | D． | 10（$\sqrt{6}$-$\sqrt{2}$） |
分析 由题意可得AB=20，∠BAC=30°，∠ABC=75°，由三角形内角和定理可得∠ACB=75°，由正弦定理得BC=$\frac{20sin30°}{sin75°}$=10（$\sqrt{6}$-$\sqrt{2}$） km．
解答 解：如图，由题意可得AB=20，∠BAC=30°，∠ABC=75°
所以，∠ACB=75°，由正弦定理得BC=$\frac{20sin30°}{sin75°}$=10（$\sqrt{6}$-$\sqrt{2}$） km，
故缉私艇B与船C的距离为10（$\sqrt{6}$-$\sqrt{2}$） km．
故选D．
点评 本题考查三角形内角和定理，正弦定理的应用，求出AB=20，∠BAC=30°，∠ABC=75°，是解题的关键．
练习册系列答案
一本好题口算题卡系列答案
相关题目
19．曲线y=x2的一种参数方程是（ ）
| A． | $\left\{{\begin{array}{l}{x={t^2}}\\{y={t^4}}\end{array}}\right.$ | B． | $\left\{{\begin{array}{l}{x=sint}\\{y={{sin}^2}t}\end{array}}\right.$ | C． | $\left\{{\begin{array}{l}{x=\sqrt{t}}\\{y=t}\end{array}}\right.$ | D． | $\left\{{\begin{array}{l}{x=t}\\{y={t^2}}\end{array}}\right.$ |
16．下列推理是演绎推理的是（ ）
| A． | 由 ${a_1}=1，{a_{n+1}}=\frac{a_n}{{1+{a_n}}}$，因为${a_1}=1，{a_2}=\frac{1}{2}，{a_3}=\frac{1}{3}，{a_4}=\frac{1}{4}$，故有${a_n}=\frac{1}{n}（n∈{N^*}）$ | |
| B． | 科学家利用鱼的沉浮原理制造潜艇 | |
| C． | 妲己惑纣王，商灭；西施迷吴王，吴灭；杨贵妃迷唐玄宗，致安史之乱，故曰：“红颜祸水也” | |
| D． | 《论语•学路》篇中说：“名不正，则言不顺；言不顺，则事不成；事不成，则礼乐不兴；礼乐不兴，则刑罚不中；刑罚不中，则民无所措手足；所以，名不正，则民无所措手足”． |
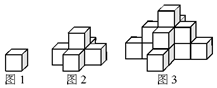图1是一个水平摆放的小正方体木块，图2，图3是由这样的小正方体木块叠放而成的，按照这样的规律放下去，至第六个叠放的图形中，小正方体木块总数就是（ ）
《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑，如图，网格纸上正方形小格的边长为1，图中粗线画出的是某几何体毛坯的三视图，第一次切削，将该毛坯得到一个表面积最大的长方体，第二次切削沿长方体的对角面刨开，得到两个三棱柱，第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马，则阳马与鳖臑的体积之比为（ ）