题目内容
已知动圆M与圆C1：(x＋4)2＋y2＝2外切，与圆C2：(x－4)2＋y2＝2内切，求动圆圆心M的轨迹方程．
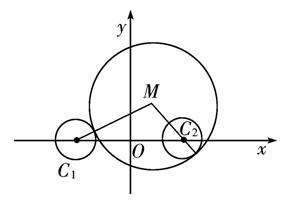
解析：设动圆M的半径为r，
则由已知|MC1|＝r＋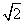
，|MC2|＝r－，
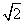∴|MC1|－|MC2|＝2.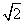
又C1(－4,0)，C2(4,0)，∴|C1C2|＝8，
∴2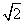＜|C1C2|.
根据双曲线定义知，点M的轨迹是以C1(－4,0)，C2(4,0)为焦点的双曲线的右支．
∵a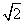＝，c＝4，∴b2＝c2－a2＝14，
∴
点M的轨迹方程是
－
＝1(x≥)．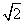
练习册系列答案
相关题目
P在曲线C2上，且直线l与椭圆C1有公共点，求椭圆C1的长轴长取得最小值时的椭圆方程．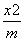
－
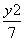＝1，直线l过其左焦点F1，交双曲线左支于A，B两点，且|AB|＝4，F2为双曲线的右焦点，△ABF2的周长为20，则m的值为( )
B．(x－1)2＋(y－2)2＝100
_________．
)，b＝(kx，y＋
)求轨迹T的方程，并说明该方程表示的曲线的形状．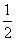
时，已知点B(0，－