题目内容
在平面直角坐标系中，已知向量a＝(x，y－
)，b＝(kx，y＋)(k∈R)，a⊥b，动点M(x，y)的轨迹为T.
(1
)求轨迹T的方程，并说明该方程表示的曲线的形状．
(2)当k＝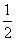
时，已知点B(0，－)，是否存在直线l：y＝x＋m ，使点B关于直线l的对称点落在轨迹T上？若存在，求出直线l的方程；若不存在，请说明理由．
解析：(1)∵a⊥b，∴ a·b＝(x，y－)·(kx，y＋)＝0，得kx2＋y2－2＝0，即kx2＋y2＝2.
当k＝0时，方程表示两条与x轴平行的直线；
当k＝1时，方程表示以原点为圆心，以为半径的圆；
当k＞0且k≠1时，方程表示椭圆；
当k＜0时，方程表示焦点在y轴上的双曲线．
(2)当k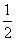＝时，动点M的轨迹T的方程为
＋
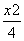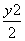＝1，
设满足条件的直线l存在，点B关于直线l的对称点为B′(x0，y0)，则由BB′⊥l得，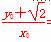
＝－1，由BB′的中点在l上得
＝
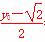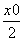＋m，解得x0＝－－m，y0＝m.
∵点B′(x0，y0)在椭圆上，∴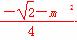
＋
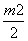＝1.整理得3m2＋2m－2＝0，解得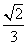m＝
或m＝－.
∴直线l的方程为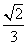y＝x＋或y＝x－.
经检验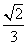y＝x＋和y＝x－都符合题设．∴满足条件的直线l存在，其方程为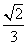y＝x＋或y＝x－.
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
线y2＝4x的焦点为F，准线为l，P为抛物线上一点，
直线x－2y－3＝0上，求圆的方程．
－
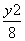＝1(x>1) B．x2－
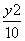＝1(x>1)
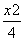＋y2＝1，F1，F2为其两焦点，P为椭圆上任一点．则|PF1|·|PF2|的最大值为( )
＋
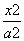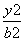＝1(a＞b＞0)上一点P，F1、F2为椭圆
的焦点，若∠F1PF2＝θ，则△PF1F2的面积等于________．