题目内容
在平面直角坐标系内,动圆C过定点F(1,0),且与定直线x=-1相切.
(1)求动圆圆心C的轨迹C2的方程;
(2)中心在O的椭圆C1的一个焦点为F,直线l过点M(4,0).若坐标原点O关于直线l的对称点 P在曲线C2上,且直线l与椭圆C1有公共点,求椭圆C1的长轴长取得最小值时的椭圆方程.
P在曲线C2上,且直线l与椭圆C1有公共点,求椭圆C1的长轴长取得最小值时的椭圆方程.
解析:(1)因为圆心C到定点F(1,0)的距离与到定直线x=-1的距离相等.
所以由抛物线定义知,C的轨迹C2是以F(1,0)为焦点,
直线x=-1为准线的抛物线,所以动圆圆心C的轨迹C2的方程为y2=4x.
(2)设P(m,n),直线l方程为y=k(x-4),则OP中点为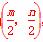 ,
,
∵O、P两点关于直线y=k(x-4)对称,
∴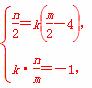 即
即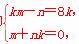 解得
解得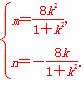
将其代入抛物线方程,得: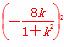 =4×
=4×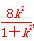 ,解得k2=1.
,解得k2=1.
设椭圆C1的方程为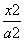 +
+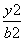 =1,
=1,
联列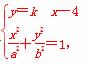 消去y得:(a2+b2)x2-8a2x+16a2-a2b2=0,
消去y得:(a2+b2)x2-8a2x+16a2-a2b2=0,
由Δ=(- 8a2)2-4(a2+b2)(16a2-a2b2)≥0,
8a2)2-4(a2+b2)(16a2-a2b2)≥0,
得a2+b2≥16,
注意到b2=a2-1,即2a2≥17,可得a≥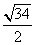 ,即2a≥
,即2a≥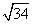 ,
,
因此,椭圆C1长轴长的最小值为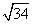 ,此时椭圆的方程为
,此时椭圆的方程为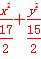 =1.
=1.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 ,且下列四个关系:
,且下列四个关系: ; ②
; ②  ; ③
; ③  ; ④
; ④  .
. 的个数是 .
的个数是 .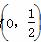 的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为2
的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为2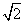 时,求直线m的方程.
时,求直线m的方程.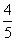 ,则C的离心率为( )
,则C的离心率为( )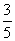 B.
B.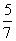 C.
C.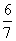
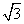 y+4=0相切.
y+4=0相切. 圆
圆 内的动点P使
内的动点P使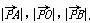 成等比数列,求
成等比数列,求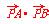 的
的 取值范围.
取值范围. 直线x-2y-3=0上,求圆的方程.
直线x-2y-3=0上,求圆的方程.