题目内容

一个袋中装有大小相同的黑球和白球共9个，从中任取2个球，记随机变量X为取出2球中白球的个数，已知P（X=2）=
5
12
．
（Ⅰ）求袋中白球的个数；
（Ⅱ）求随机变量X的分布列及其数学期望．
考点：离散型随机变量的期望与方差
专题：计算题,概率与统计
分析：（I）设袋中有白球n个，利用古典概型的概率计算公式即可得到P（X=2）=
C
2
n
C
2
9
=
5
12
，解出即可；
（II）由（I）可知：袋中共有3个黑球，6个白球．随机变量X的取值为0，1，2，3，求出相应的概率，即可得出随机变量X的分布列及其数学期望．
解答： 解：（Ⅰ）设袋中有白球n个，则P（X=2）=
C
2
n
C
2
9
=
5
12
，解得n=6．
（Ⅱ）由（I）可知：袋中共有3个黑球，6个白球．
随机变量X的取值为0，1，2，则P（X=0）=
C
2
3
C
2
9
=
1
12
，P（X=1）=
C
1
3
C
1
6
C
2
9
=
1
2
，P（X=2）=
5
12
．
随机变量X的分布列如下：
X 0 1 2
P
1
12
1
2
5
12
EX=0×
1
12
+1×
1
2
+2×
5
12
=
4
3
．
点评：熟练掌握古典概型的概率计算公式和超几何分布的概率计算公式是解题的关键．
练习册系列答案
相关题目
已知函数f（x）=4x-cosx，则f（x）在[0，2π]上的零点个数是（　　）
A、1B、2C、3D、4
已知数列{an}和{bn}满足：a1=λ，an+1=
2
3
an+n-4，bn=（-1）n（an-3n+21），其中λ为实数，n为正整数．
（1）对任意实数λ，求证：a1，a2，a3不成等比数列；
（2）试判断数列{bn}是否为等比数列，并证明你的结论；
（3）设Sn为数列{bn}的前n项和．是否存在实数λ，使得对任意正整数n，都有Sn＞-12？若存在，求λ的取值范围；若不存在，说明理由．
已知向量
a
=（sinx，cosx），
b
=（6sinx+cosx，7sinx-2cosx）．设函数f（x）=
a
•
b
．
（Ⅰ）求函数f（x）的最大值及此时x的取值集合；
（Ⅱ）在角A为锐角的△ABC中，角A、B、C的对边分别为a、b、c，f（A）=6且△ABC的面积为3，b+c=2+3
2
，求a的值．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
1
2
，点（1，
3
2
）在椭圆C上．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若椭圆C的两条切线交于点M（4，t），其中t∈R，切点分别是A、B，试利用结论：在椭圆
x2
a2
+
y2
b2
=1上的点（x0，y0）处的椭圆切线方程是
x0x
a2
+
y0y
b2
=1，证明直线AB恒过椭圆的右焦点F2；
（Ⅲ）试探究
1
|AF2|
+
1
|BF2|
的值是否恒为常数，若是，求出此常数；若不是，请说明理由．
阅读：已知a、b∈（0，+∞），a+b=1，求y=
1
a
+
2
b
的最小值．解法如下：y=
1
a
+
2
b
=（
1
a
+
2
b
）（a+b）=
b
a
+
2a
b
+3≥3+2
2
，当且仅当
b
a
=
2a
b
，即a=
2
-1，b=2-
2
时取到等号，则y=
1
a
+
2
b
的最小值为3+2
2
．应用上述解法，求解下列问题：
（1）已知a，b，c∈（0，+∞），a+b+c=1，求y=
1
a
+
1
b
+
1
c
的最小值；
（2）已知x∈（0，
1
2
），求函数y=
1
x
+
8
1-2x
的最小值；
（3）已知正数a1、a2、a3，…，an，a1+a2+a3+…+an=1，求证：S=
a12
a1+a2
+
a22
a2+a3
+
a32
a3+a4
+…+
an2
an+a1
≥
1
2
．
甲地区有10名人大代表，其中有4名女性；乙地区有5名人大代表，其中有3名女性，现采用分层抽样法从甲、乙两地区共抽取3名代表进行座谈．
（Ⅰ）求从甲、乙两地区各抽取的代表数；
（Ⅱ）求从甲组抽取的代表中至少有1名女性的概率；
（Ⅲ）记ξ表示抽取的3名代表中女性数，求ξ的分布列及数学期望．
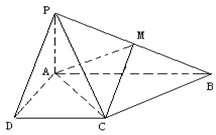已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=
1
2
，AB=1，M是PB的中点．
（Ⅰ）证明：面PAD⊥面PCD；
（Ⅱ）求AC与PB所成的角；
（Ⅲ）求面AMC与面BMC所成二面角的大小余弦值．
已知复数z=（2m2-3m-2）+（m2-3m+2）i．
（Ⅰ）当实数m取什么值时，复数z是：
①实数； 
②纯虚数；
（Ⅱ）当m=0时，化简
z2
z+5+2i
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网