题目内容
已知数列{an}和{bn}满足:a1=λ,an+1=
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
(1)对任意实数λ,求证:a1,a2,a3不成等比数列;
(2)试判断数列{bn}是否为等比数列,并证明你的结论;
(3)设Sn为数列{bn}的前n项和.是否存在实数λ,使得对任意正整数n,都有Sn>-12?若存在,求λ的取值范围;若不存在,说明理由.
| 2 |
| 3 |
(1)对任意实数λ,求证:a1,a2,a3不成等比数列;
(2)试判断数列{bn}是否为等比数列,并证明你的结论;
(3)设Sn为数列{bn}的前n项和.是否存在实数λ,使得对任意正整数n,都有Sn>-12?若存在,求λ的取值范围;若不存在,说明理由.
考点:数列与不等式的综合,数列递推式
专题:点列、递归数列与数学归纳法
分析:(1)利用反证法结合等比数列的性质和公式即可证明a1,a2,a3不成等比数列;
(2)根据等比数列的定义和性质进行证明即可;
(3)求出数列的和,解不等式即可得到结论.
(2)根据等比数列的定义和性质进行证明即可;
(3)求出数列的和,解不等式即可得到结论.
解答:
解(1)证明:假设存在一个实数λ,使a1,a2,a3是等比数列,则有a22=a1a3,
即(
λ-3)2=λ(
λ-4),
则
λ2-4λ+9=
λ2-4λ,
即9=0矛盾.
所以a1,a2,a3不成等比数列.
(2)因为bn+1=(-1)n+1[an+1-3(n+1)+21]=(-1)n+1(
an-2n+14)=
=(-1)n(an-3n+21)=-
bn,
又b1=-(λ+18),
所以当λ=-18,bn=b1=0,(n为正整数),此时{bn}不是等比数列.…8分
当λ≠-18时,b1≠0,由上式可知bn≠0,
∴
=-
(n为正整数),
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,-
为公比的等比数列.
(3)由(2)知,当λ=-18时,bn=0,则Sn=0,所以Sn>-12恒成立.
当λ≠-18,得bn=-(λ+18)(-
)n-1,
于是Sn=-
(λ+18)[1-(-
)n],
要使对任意正整数n,都有Sn>-12成立,即-
(λ+18)[1-(-
)n]>-12,
即λ<
-18,
令f(n)=1-(-
)n,
则当n为正奇数时,1<f(n)≤
,
当n为正偶数时,
≤f(n)<1,
∴f(n)的最大值为f1)=
,
于是可得λ<20×
-18=-6,
综上所述,存在实数λ∈(-∞,-6),使得对任意正整数n,都有Sn>-12.
即(
| 2 |
| 3 |
| 4 |
| 9 |
则
| 4 |
| 9 |
| 4 |
| 9 |
即9=0矛盾.
所以a1,a2,a3不成等比数列.
(2)因为bn+1=(-1)n+1[an+1-3(n+1)+21]=(-1)n+1(
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
又b1=-(λ+18),
所以当λ=-18,bn=b1=0,(n为正整数),此时{bn}不是等比数列.…8分
当λ≠-18时,b1≠0,由上式可知bn≠0,
∴
| bn+1 |
| bn |
| 2 |
| 3 |
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,-
| 2 |
| 3 |
(3)由(2)知,当λ=-18时,bn=0,则Sn=0,所以Sn>-12恒成立.
当λ≠-18,得bn=-(λ+18)(-
| 2 |
| 3 |
于是Sn=-
| 3 |
| 5 |
| 2 |
| 3 |
要使对任意正整数n,都有Sn>-12成立,即-
| 3 |
| 5 |
| 2 |
| 3 |
即λ<
| 20 | ||
1-(-
|
令f(n)=1-(-
| 2 |
| 3 |
则当n为正奇数时,1<f(n)≤
| 5 |
| 3 |
当n为正偶数时,
| 5 |
| 9 |
∴f(n)的最大值为f1)=
| 5 |
| 3 |
于是可得λ<20×
| 3 |
| 5 |
综上所述,存在实数λ∈(-∞,-6),使得对任意正整数n,都有Sn>-12.
点评:本题主要考查等比数列的判断和应用,以及数列和不等式的应用,综合性较强,运算量较大,有一定的难度.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
化简
+
+
=( )
| AC |
| CD |
| DA |
A、
| ||
B、
| ||
C、
| ||
D、
|
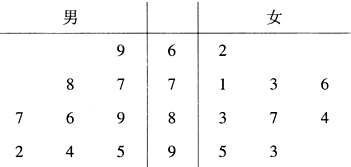 某中学招聘教师有笔试、面试两个环节,笔试成绩超过85分者才能进入面试环节,现已记录前来应聘的9位男教师和9位女教师的笔试成绩,成绩用茎叶图表示如图所示.
某中学招聘教师有笔试、面试两个环节,笔试成绩超过85分者才能进入面试环节,现已记录前来应聘的9位男教师和9位女教师的笔试成绩,成绩用茎叶图表示如图所示.