题目内容
下列不等式一定成立的是( )
A、lg(x2+
| ||||
B、
| ||||
| C、x2+1≥2|x|(x∈R) | ||||
D、
|
考点:基本不等式
专题:不等式的解法及应用
分析:A.当x=
时,lg(x2+
)=lgx;
B.
=
+
,令
=t≥2,则f(t)=t+
,利用导数研究函数的单调性即可得出;
C.由(|x|-1)2≥0,可得x2+1≥2|x|.
D.由于x2≥0,可得
≤1.
| 1 |
| 2 |
| 1 |
| 4 |
B.
| x2+4+1 | ||
|
| x2+4 |
| 1 | ||
|
| x2+4 |
| 1 |
| t |
C.由(|x|-1)2≥0,可得x2+1≥2|x|.
D.由于x2≥0,可得
| 1 |
| x2+1 |
解答:
解:A.当x=
时,lg(x2+
)=lgx,因此不成立;
B.
=
+
,
令
=t≥2,则f(t)=t+
,f′(t)=1-
=
>0.
∴f(t)≥2+
=
,因此不正确.
C.∵(|x|-1)2≥0,∴x2+1≥2|x|,正确.
D.∵x2≥0,∴
≤1,因此不正确.
故选:C.
| 1 |
| 2 |
| 1 |
| 4 |
B.
| x2+4+1 | ||
|
| x2+4 |
| 1 | ||
|
令
| x2+4 |
| 1 |
| t |
| 1 |
| t2 |
| t2-1 |
| t2 |
∴f(t)≥2+
| 1 |
| 2 |
| 5 |
| 2 |
C.∵(|x|-1)2≥0,∴x2+1≥2|x|,正确.
D.∵x2≥0,∴
| 1 |
| x2+1 |
故选:C.
点评:本题考查了基本不等式的性质、利用导数研究函数的单调性,使用基本不等式时注意“一正二定三相等”的法则,属于基础题.

练习册系列答案
相关题目
已知△ABC内角A、B、C的对边分别是a、b、c,若cosB=
,b=2,sinC=2sinA,则△ABC的面积为( )
| 1 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
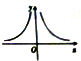 已知幂函数f(x)=xn-2(n∈N)的图象如图所示,则y=f(x)在x=1处的切线与两坐标轴围成的面积为( )
已知幂函数f(x)=xn-2(n∈N)的图象如图所示,则y=f(x)在x=1处的切线与两坐标轴围成的面积为( )A、
| ||
B、
| ||
C、
| ||
| D、4 |