题目内容
17.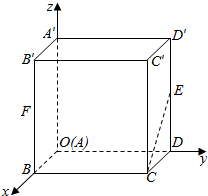 如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离.
如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离.
分析 求出点的坐标,可得$\overrightarrow{CE}$=-$\overrightarrow{A′F}$,即可证明CE∥A′F,利用平面A′B与平面D′C的距离为2,可得CE与A′F之间的距离.
解答 证明:由题意,A′(0,0,2),F(1,0,1),C(1,2,0),E(0,2,1),
∴$\overrightarrow{CE}$=(-1,0,1),$\overrightarrow{A′F}$=(1,0,-1),
∴$\overrightarrow{CE}$=-$\overrightarrow{A′F}$,
∴CE∥A′F,
∵平面A′B与平面D′C的距离为2,
∴CE与A′F之间的距离为2.
点评 本题考查向量知识的运用,考查学生的计算能力,正确求出向量的坐标是关键.

练习册系列答案
相关题目
7.已知命题p:函数y=2-ax+1(a>0,a≠1)恒过定点(-1,1):命题q:若函数f(x-1)为偶函数,则f(x)的图象关于直线x=1对称.下列命题为真命题的是( )
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
5.“抛物线y=ax2的准线方程为y=2”是“抛物线y=ax2的焦点与双曲线$\frac{y^2}{3}-{x^2}=1$的焦点重合”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.已知复数$z=\frac{2}{-1+i}$,则( )
| A. | z的共轭复数为1+i | B. | z的实部为1 | ||
| C. | |z|=2 | D. | z的虚部为-1 |