题目内容
7.圆O1的方程为x2+(y+1)2=4.圆O2的圆心O2(2,1).(1)若圆O2与圆O1外切.求圆O2的方程.并求内公切线方程;
(2)若圆O2与圆O1交于A、B两点,且|AB|=2$\sqrt{2}$,求圆O2的方程.
分析 (1)通过圆心距对于半径和,求出圆的半径,即可求出圆的方程,两圆方程相减,即得两圆内公切线的方程.
(2)利用圆心距与写出的故选求出,圆到直线的距离,然后求出所求圆的半径,即可求出圆的方程.
解答 解:(1)圆O1的方程为x2+(y+1)2=4,圆心坐标(0,-1),半径为:2,
圆O2的圆心O2(2,1).
圆心距为:$\sqrt{4+4}$=2$\sqrt{2}$,圆O2与圆O1外切,
所求圆的半径为:2$\sqrt{2}$-2,
圆O2的方程(x-2)2+(y-1)2=12-8$\sqrt{2}$,
两圆方程相减,即得两圆内公切线的方程为x+y+1-2$\sqrt{2}$=0.
(2)圆O2与圆O1交于A、B两点,且|AB|=2$\sqrt{2}$.
所以圆O1交到AB的距离为:$\sqrt{4-2}$=$\sqrt{2}$,
当圆O2到AB的距离为:$\sqrt{2}$,
圆O2的半径为:$\sqrt{2+2}$=2.
圆O2的方程:(x-2)2+(y-1)2=4.
当圆O2到AB的距离为:3$\sqrt{2}$,
圆O2的半径为:$\sqrt{18+2}$=$\sqrt{20}$.
圆O2的方程:(x-2)2+(y-1)2=20.
综上:圆O2的方程:(x-2)2+(y-1)2=4或(x-2)2+(y-1)2=20.
点评 本题考查两个圆的位置关系,圆的方程的求法,考查计算能力.

练习册系列答案
相关题目
19.若点p在抛物线y2=2x上,A(a,0)
(1)请你完成下表:
(2)若α∈R,求|PA|的最小值及相应的点P坐标.
(1)请你完成下表:
| 实物a的值 | -2 | 0 | 0.5 | 1 | 2 |
| |PA|的最小值 | 0 | ||||
| 相应的点P坐标 |
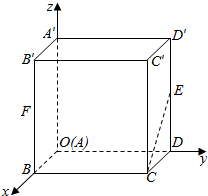 如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离.
如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离.