题目内容
6.函数$y={a^{{x^2}-3x+2}}({a>1})$的单调增区间是[$\frac{3}{2}$,+∞).分析 令t=x2-3x+2,则函数即y=at,根据a>1时,本题即求函数t的增区间,利用二次函数的性质可得t的增区间.
解答 解:令t=x2-3x+2,则函数即y=at,
根据a>1时,本题即求函数t的增区间,
利用二次函数的性质可得t的增区间为[$\frac{3}{2}$,+∞),
故答案为:$[{\frac{3}{2},+∞})$.
点评 本题主要考查指数函数、二次函数的性质,复合函数的单调性,属于中档题.

练习册系列答案
相关题目
1.在△ABC中,已知角A,B,C的对边分别为a,b,c.若a=2,A=30°,C=45°,则△ABC的面积为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$+1 | C. | $\frac{1}{2}$($\sqrt{3}$+1) | D. | 2$\sqrt{2}$ |
11.点M为棱长是2$\sqrt{2}$的正方体ABCD-A1B1C1D1的内切球O球面上的动点,点N为B1C1的中点,若满足DM⊥BN,则动点M的轨迹的长度为( )
| A. | $\frac{{2\sqrt{5}π}}{5}$ | B. | $\frac{{4\sqrt{5}π}}{5}$ | C. | $\frac{{2\sqrt{10}π}}{5}$ | D. | $\frac{{4\sqrt{10}π}}{5}$ |
16.化简 $\overrightarrow{AC}-\overrightarrow{BD}+\overrightarrow{CD}-\overrightarrow{AB}$=( )
| A. | $\overrightarrow{AB}$ | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{DA}$ | D. | $\overrightarrow 0$ |
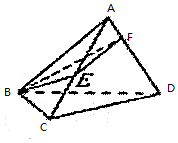 如图,在正四面体A-BCD中,所有棱长为1,E,F分别是AC,AD上的动点,求截面△BEF周长的最小值.
如图,在正四面体A-BCD中,所有棱长为1,E,F分别是AC,AD上的动点,求截面△BEF周长的最小值.