题目内容
5.已知椭圆的中心在原点,焦点为F1(0,-2$\sqrt{2}$),F2(0,2$\sqrt{2}$),且离心率e=$\frac{2\sqrt{2}}{3}$.(1)求椭圆的方程;
(2)直线l(与坐标轴不平行)与椭圆交于不同的两点A、B,且线段AB中点的横坐标为-$\frac{1}{2}$,求直线l斜率的取值范围.
分析 (1)设椭圆的标准方程,由c,及离心率即可求得a值,则b2=a2-c2=1,即可求得椭圆方程;
(2)将直线方程代入椭圆方程,由韦达定理及中点坐标公式可知$\left\{\begin{array}{l}{△>0}\\{\frac{{x}_{1}+{x}_{2}}{2}=-\frac{1}{2}}\end{array}\right.$,即可求得直线l斜率的取值范围.
解答 解:(1)设椭圆方程为$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$(a>b>0),由已知c=2$\sqrt{2}$,e=$\frac{c}{a}$=$\frac{2\sqrt{2}}{3}$,
解得:a=3,则b2=a2-c2=1,
故所求方程为$\frac{{y}^{2}}{9}+{x}^{2}=1$;(6分)
(2)设直线l的方程为y=kx+t(k≠0),A(x1,y1),B(x2,y2),
代入椭圆方程$\left\{\begin{array}{l}{y=kx+t}\\{\frac{{y}^{2}}{9}+{x}^{2}=1}\end{array}\right.$,整理得(k2+9)x2+2ktx+t2-9=0,
由韦达定理可知:x1+x2=-$\frac{2kt}{{k}^{2}+9}$,
由题意得$\left\{\begin{array}{l}{△>0}\\{\frac{{x}_{1}+{x}_{2}}{2}=-\frac{1}{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{4{k}^{2}{t}^{2}-4({k}^{2}+9)({t}^{2}-9)>0}\\{-\frac{2kt}{{k}^{2}+9}=-1}\end{array}\right.$,
解得:k>$\sqrt{3}$或k<-$\sqrt{3}$.
直线l斜率的取值范围(-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞).(12分
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,考查韦达定理,中点坐标公式,考查计算能力,属于中档题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案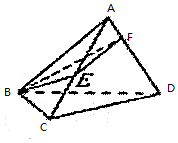 如图,在正四面体A-BCD中,所有棱长为1,E,F分别是AC,AD上的动点,求截面△BEF周长的最小值.
如图,在正四面体A-BCD中,所有棱长为1,E,F分别是AC,AD上的动点,求截面△BEF周长的最小值.