题目内容
11.设函数f(x)=e2x+ax在(0,+∞)上单调递增,则实数a的取值范围为( )| A. | [-1,+∞) | B. | (-1,+∞) | C. | [-2,+∞) | D. | (-2,+∞) |
分析 求导,由题意可知f′(x)≥0恒成立,由指数函数的性质,即可求得实数a的取值范围.
解答 解:由函数f(x)=e2x+ax在(0,+∞)上单调递增,则f′(x)≥0恒成立,
∴f′(x)=2e2x+a,即a≥-2e2x,x∈(0,+∞),
由e2x>0,则-2e2x<-2,
则a≥-2,
故选:C.
点评 本题考查导数的综合应用,考查导数与函数单调性的应用,指数函数的性质,考查计算能力,属于中档题.

练习册系列答案
相关题目
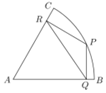 如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.
如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.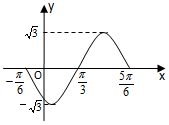 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期上的图象如图所示,
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期上的图象如图所示,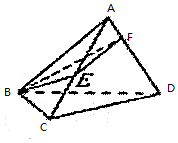 如图,在正四面体A-BCD中,所有棱长为1,E,F分别是AC,AD上的动点,求截面△BEF周长的最小值.
如图,在正四面体A-BCD中,所有棱长为1,E,F分别是AC,AD上的动点,求截面△BEF周长的最小值.