题目内容
15.设函数f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}},|x|≤1}\\{|x|,|x|>1}\end{array}\right.$,若方程f(x)=a有且只有一个实根,则实数a的值是1.分析 作函数f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}},|x|≤1}\\{|x|,|x|>1}\end{array}\right.$的图象,从而化方程的解与函数的图象的交点.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}},|x|≤1}\\{|x|,|x|>1}\end{array}\right.$的图象如下,
结合图象可知,当a=1时,
方程f(x)=a有且只有一个实根,
故答案为:1.
点评 本题考查了方程的根与函数的零点的关系应用及数形结合的思想应用.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
6.某年青教师近五年内所带班级的数学平均成绩统计数据如表:
(1)利用所给数据,求出平均分与年份之间的回归直线方程$\hat y=bx+a$
(2)利用(1)中所求出的直线方程预测该教师2015年所带班级的数学平均成绩.
参考公式:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 年份x年 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 平均成绩y分 | 97 | 98 | 103 | 108 | 109 |
(2)利用(1)中所求出的直线方程预测该教师2015年所带班级的数学平均成绩.
参考公式:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.
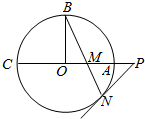 如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P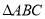 中,
中,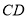 是
是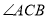 的角平分线,
的角平分线,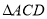 的外接圆交
的外接圆交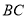 于
于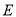 点.
点.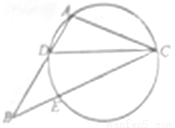
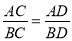 ;
;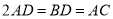 ,求
,求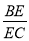 的值.
的值.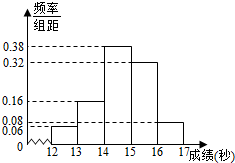 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.